The Area of any Irregular Quadrilateral

A plane figure bounded by four straight line segments is called an irregular quadrilateral. The area of any irregular quadrilateral can be calculated by dividing it into triangles.

 

Example:

Find the area of a quadrilateral $ABCD$ whose sides are $9$ m, $40$ m, $28$ m and $15$ m respectively and the angle between the first two sides is a right angle.

 

Solution:

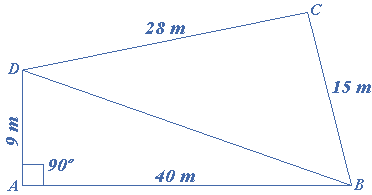
From the figure we notice that $ABD$ is a right-angled triangle, in which $AB = 40$ m, $AD = 9$ m. Also

$$\begin{gathered} B{D^2} = A{B^2} + A{D^2} \\ B{D^2} = {40^2} + {9^2} \\ BD = \sqrt {{{40}^2} + {9^2}} = \sqrt {1681} = 41 \\ \end{gathered}$$

Now, the area of $\Delta ABD = \frac{1}{2} \times 40 \times 9 = 180$ m
In $\Delta BCD$, $BD = a = 41$ m, $DC = b = 28$ m, $CB = c = 15$ m
$\therefore s = \frac{{a + b + c}}{2} = \frac{{41 + 28 + 15}}{2} = 42$ m

Now,

$$\begin{gathered} {\text{Area}}\,{\text{of}}\,\Delta BCD = \sqrt {s(s - a)(s - b)(s - c)} \, \\ {\text{Area}}\,{\text{of}}\,\Delta BCD = \sqrt {42(42 - 41)(42 - 28)(42 - 15)} = \sqrt {42 \times 14 \times 27} = 126\,sq\,m \\ \end{gathered}$$

The area of the quadrilateral $ABCD$$=$ area of $\Delta ABD$ $+$area of $\Delta BCD$
The area of the quadrilateral $ABCD$ $= (180 + 126) = 306$ square meters.

 

Example:

In a quadrilateral the diagonal is $42$ cm and the two perpendiculars on it from the other vertices are $8$ cm and $9$ cm respectively. Find the area of the quadrilateral.

 

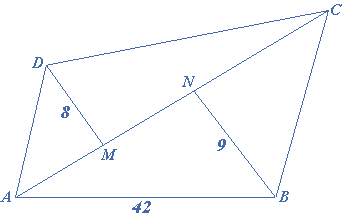
Solution:

Given that from the figure $AC = 42$ m, $BN = 9$ m, $DM = 8$ m
The area of $ABCD =$ area of $\Delta ABC +$area of $\Delta ACD$
The area of $ABCD$$= \frac{1}{2} \times 9 \times 42 + \frac{1}{2} \times 8 \times 42 = 189 + 168 = 357$ square meters.