The Area of any Irregular Quadrilateral

A plane figure bounded by four straight line segments is called an irregular quadrilateral. The area of any irregular quadrilateral can be calculated by dividing it into triangles.

 

Example:

Find the area of a quadrilateral $$ABCD$$ whose sides are $$9$$ m, $$40$$ m, $$28$$ m and $$15$$ m respectively and the angle between the first two sides is a right angle.

 

Solution:

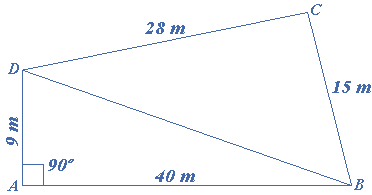
From the figure we notice that $$ABD$$ is a right-angled triangle, in which $$AB = 40$$ m, $$AD = 9$$ m. Also
\[\begin{gathered} B{D^2} = A{B^2} + A{D^2} \\ B{D^2} = {40^2} + {9^2} \\ BD = \sqrt {{{40}^2} + {9^2}} = \sqrt {1681} = 41 \\ \end{gathered} \]

Now, the area of $$\Delta ABD = \frac{1}{2} \times 40 \times 9 = 180$$ m
In $$\Delta BCD$$, $$BD = a = 41$$ m, $$DC = b = 28$$ m, $$CB = c = 15$$ m
$$\therefore s = \frac{{a + b + c}}{2} = \frac{{41 + 28 + 15}}{2} = 42$$ m

Now,
\[\begin{gathered} {\text{Area}}\,{\text{of}}\,\Delta BCD = \sqrt {s(s – a)(s – b)(s – c)} \, \\ {\text{Area}}\,{\text{of}}\,\Delta BCD = \sqrt {42(42 – 41)(42 – 28)(42 – 15)} = \sqrt {42 \times 14 \times 27} = 126\,sq\,m \\ \end{gathered} \]

The area of the quadrilateral $$ABCD$$$$ = $$ area of $$\Delta ABD$$ $$ + $$area of $$\Delta BCD$$
The area of the quadrilateral $$ABCD$$ $$ = (180 + 126) = 306$$ square meters.

 

Example:

In a quadrilateral the diagonal is $$42$$ cm and the two perpendiculars on it from the other vertices are $$8$$ cm and $$9$$ cm respectively. Find the area of the quadrilateral.

 

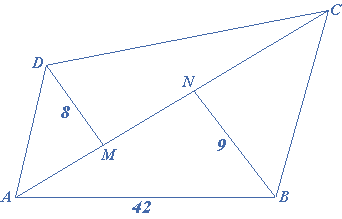
Solution:

Given that from the figure $$AC = 42$$ m, $$BN = 9$$ m, $$DM = 8$$ m
The area of $$ABCD = $$ area of $$\Delta ABC + $$area of $$\Delta ACD$$
The area of $$ABCD$$$$ = \frac{1}{2} \times 9 \times 42 + \frac{1}{2} \times 8 \times 42 = 189 + 168 = 357$$ square meters.