The Area of a Cyclic Quadrilateral
A quadrilateral inscribed is a circle is known as a cyclic quadrilateral. The proof is beyond the scope of this tutorial and will be discussed in an advanced tutorial, so only the formula is given here for application.
If $$a$$, $$b$$, $$c$$ and $$d$$ are the sides of a cyclic quadrilateral and if $$s = \frac{{a + b + c + d}}{2}$$, then
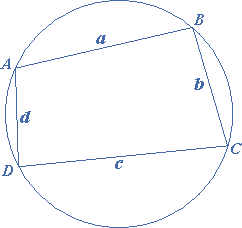
The area of a cyclic quadrilateral $$ = \sqrt {(s – a)(s – b)(s – c)(s – d)} $$
Example:
In a circular grassy plot, a quadrilateral shape with its corners touching the boundary of the plot is to be paved with bricks. Find the area of the quadrilateral when the sides of the quadrilateral are $$36$$ m, $$77$$ m, $$75$$ m and $$40$$ m.
Solution:
Given that the sides of the quadrilateral are $$a = 36$$m, $$b = 77$$m, $$c = 75$$m and $$d = 40$$m
\[s = \frac{{a + b + c + d}}{2} = \frac{{36 + 77 + 75 + 40}}{2} = \frac{{228}}{2} = 114m\]
The area of the cyclic quadrilateral $$ = \sqrt {(s – a)(s – b)(s – c)(s – d)} $$
The area of the cyclic quadrilateral $$ = \sqrt {(114 – 36)(114 – 77)(114 – 75)(114 – 40)} $$
The area of the cyclic quadrilateral $$ = \sqrt {78 \times 37 \times 39 \times 74} = 39 \times 37 \times 2 = 2886$$ square meters.
