Two Circles Touching Internally
If two given circles are touching each other internally, use this example to understand the concept of internally toucheing circles.
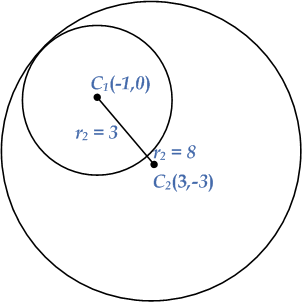
Consider the given circles
$${x^2} + {y^2} + 2x – 8 = 0\,\,\,{\text{ – – – }}\left( {\text{i}} \right)$$ and $${x^2} + {y^2} – 6x + 6y – 46 = 0\,\,\,{\text{ – – – }}\left( {{\text{ii}}} \right)$$
Let $${C_1}$$ and $${r_1}$$ be the center and radius of circle (i) respectively. Now to find the center and radius compare the equation of a circle with the general equation of a circle $${x^2} + {y^2} + 2gx + 2fy + c = 0$$
To get the center and radius, we have
Center $${C_1}\left( { – g, – f} \right) = {C_1}\left( { – 1,0} \right)$$
Radius $${r_1} = \sqrt {{g^2} + {f^2} – c} = \sqrt {{{\left( 1 \right)}^2} + {{\left( 0 \right)}^2} – \left( { – 8} \right)} = \sqrt {1 + 8} = \sqrt 9 = 3$$
Let $${C_2}$$ and $${r_2}$$ be the center and radius of the circle (ii) respectively. Now to find the center and radius compare the equation of a circle with the general equation of a circle $${x^2} + {y^2} + 2gx + 2fy + c = 0$$
To get the center and radius, we have
Center $${C_2}\left( { – g, – f} \right) = {C_2}\left( { – \left( { – 3} \right), – 3} \right) = {C_2}\left( {3, – 3} \right)$$
Radius $${r_2} = \sqrt {{g^2} + {f^2} – c} = \sqrt {{{\left( 3 \right)}^2} + {{\left( { – 3} \right)}^2} – \left( { – 46} \right)} = \sqrt {9 + 9 + 46} = \sqrt {64} = 8$$
Using the distance formula, we find the distance between the centers of the given circles. We have
\[\left| {{C_1}{C_2}} \right| = \sqrt {{{\left( {3 – \left( { – 1} \right)} \right)}^2} + {{\left( { – 3 – 0} \right)}^2}} = \sqrt {{{\left( {3 + 1} \right)}^2} + {{\left( { – 3} \right)}^2}} = \sqrt {16 + 9} = \sqrt {25} = 5\]
Now subtracting the radius of the second circle from the first circle, we have
\[{r_2} – {r_1} = 8 – 3 = 5\]
This shows that the distance between the centers of the given circles is equal to the difference of their radii. This is only possible if the circles touche each other internally, as shown in the given diagram.
