Equation of a Circle Given Two Points and Tangent Line

Consider the general equation a circle is given by

\[{x^2} + {y^2} + 2gx + 2fy + c = 0\,\,\,{\text{ – – – }}\left( {\text{i}} \right)\]

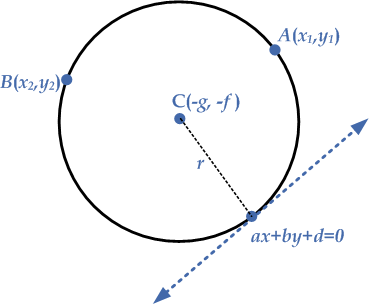
If the given circle is passing through two points, say $$A\left( {{x_1},{y_1}} \right)$$ and $$B\left( {{x_2},{y_2}} \right)$$, then these points must satisfy the general equation of a circle. Now put these two points in the given equation of a circle, i.e.:

\[\begin{gathered} {x_1}^2 + {y_1}^2 + 2g{x_1} + 2f{y_1} + c = 0\,\,\,{\text{ – – – }}\,\left( {{\text{ii}}} \right) \\ {x_2}^2 + {y_2}^2 + 2g{x_2} + 2f{y_2} + c = 0\,\,\,{\text{ – – – }}\,\left( {{\text{iii}}} \right) \\ \end{gathered} \]

Also the given straight line $$ax + by + d = 0\,\,\,{\text{ – – – }}\left( {{\text{iv}}} \right)$$ touches the circle at one point, as shown in the given diagram, and it is clear from the diagram that the distance of a given point from the center $$\left( { – g, – f} \right)$$ must be equal to the radius of the circle. By using the formula for distance between the point and the line, i.e.:

\[r = \frac{{\left| { – ag – bf + d} \right|}}{{\sqrt {{a^2} + {b^2}} }}\]

The radius of the circle in general form is $$r = \sqrt {{g^2} + {f^2} – c} $$, and using this value we get

\[ \Rightarrow \sqrt {{g^2} + {f^2} – c} = \frac{{\left| { – ag – bf + d} \right|}}{{\sqrt {{a^2} + {b^2}} }}\]

Squaring both sides of the above equation we have

\[ \Rightarrow {g^2} + {f^2} – c = \frac{{{{\left( { – ag – bf + d} \right)}^2}}}{{{a^2} + {b^2}}}\,\,\,{\text{ – – – }}\left( {\text{v}} \right)\]

To evaluate the equation of the required circle, we must the find values of $$g,f,c$$ from the above equations (ii), (iii) and (v). We can solve these three using the method of simultaneous equations, and then put all this information into equation (i) to get the required circle.

An alternate way is that we assume that the required equation of a circle is

\[{\left( {x – h} \right)^2} + {\left( {y – k} \right)^2} = {r^2}\,\,\,{\text{ – – – }}\left( {\text{i}} \right)\]

Since the circle passes through the points $$A\left( {{x_1},{y_1}} \right)$$ and $$B\left( {{x_2},{y_2}} \right)$$, these points must satisfy the above equation of a circle. So we have

\[\begin{gathered} {\left( {{x_1} – h} \right)^2} + {\left( {{y_1} – k} \right)^2} = {r^2}\,\,\,{\text{ – – – }}\left( {{\text{ii}}} \right) \\ {\left( {{x_2} – h} \right)^2} + {\left( {{y_2} – k} \right)^2} = {r^2}\,\,\,{\text{ – – – }}\left( {{\text{iii}}} \right) \\ \end{gathered} \]

The given line $$ax + by + d = 0\,\,\,{\text{ – – – }}\left( {{\text{iv}}} \right)$$ touches the circle.

So the distance to the center of the circle from the given line $$ax + by + d = 0$$ must be equal to its radius, i.e.:
\[r = \frac{{\left| {a{x_1} + b{y_1} + d} \right|}}{{\sqrt {{a^2} + {b^2}} }}\,\,\,{\text{ – – – }}\left( {\text{v}} \right)\]

Now using the above equations (ii), (iii) and (v), we can find the values of $$h,k$$ and $$r$$, and in equation (i) we get the required circle.