Distance Formula
Let $$P\left( {{x_1},{y_1}} \right)$$ and $$Q\left( {{x_2},{y_2}} \right)$$ be any two points on the line. We will find the distance between P and Q.
For this, draw PM and QN perpendicular to the X–Axis.
From P draw PR perpendicular to QN.
Consider the right angle triangle $$\Delta {\text{PQR}}{\text{.}}$$
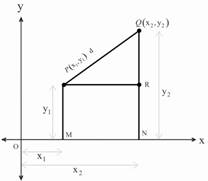
I. First we find the distance between P and R.
\[\begin{gathered} \left| {{\text{PR}}} \right|{\text{ = }}\left| {{\text{MN}}} \right| \\ \left| {{\text{PR}}} \right|{\text{ = }}\left| {{\text{ON – OM}}} \right| \\ \left| {{\text{PR}}} \right|{\text{ = }}\left| {{{\text{x}}_{\text{2}}} – {{\text{x}}_{\text{1}}}} \right| \\ \end{gathered} \]
II. Secondly, we find the distance between R and Q.
\[\begin{gathered} \left| {{\text{RQ}}} \right| = \left| {{\text{NQ – NR}}} \right| \\ \left| {{\text{RQ}}} \right| = \left| {{{\text{y}}_{\text{2}}} – {y_1}} \right| \\ \end{gathered} \]
III. Finally, we find the distance between P and Q.
By using the Pythagorean Theorem we have
\[\begin{gathered} {\left| {{\text{PQ}}} \right|^{\text{2}}}{\text{ = }}{\left| {{\text{PR}}} \right|^{\text{2}}}{\text{ + }}{\left| {{\text{PQ}}} \right|^{\text{2}}} \\ {\left| {{\text{PQ}}} \right|^{\text{2}}}{\text{ = }}{\left| {{{\text{x}}_{\text{2}}}{\text{ – }}{{\text{x}}_{\text{1}}}} \right|^{\text{2}}}{\text{ + }}{\left| {{{\text{y}}_{\text{2}}}{\text{ – }}{{\text{y}}_{\text{1}}}} \right|^{\text{2}}} \\ {\left| {{\text{PQ}}} \right|^{\text{2}}}{\text{ = }}{\left( {{{\text{x}}_{\text{2}}}{\text{ – }}{{\text{x}}_{\text{1}}}} \right)^{\text{2}}}{\text{ + }}{\left( {{{\text{y}}_{\text{2}}}{\text{ – }}{{\text{y}}_{\text{1}}}} \right)^{\text{2}}} \\ \Rightarrow \left| {{\text{PQ}}} \right|{\text{ = }}\sqrt {{{\left( {{{\text{x}}_{\text{2}}}{\text{ – }}{{\text{x}}_{\text{1}}}} \right)}^{\text{2}}}{\text{ + }}{{\left( {{{\text{y}}_{\text{2}}}{\text{ – }}{{\text{y}}_{\text{1}}}} \right)}^{\text{2}}}} \\ \end{gathered} \]
\[\boxed{{\text{d = }}\sqrt {{{\left( {{{\text{x}}_{\text{2}}}{\text{ – }}{{\text{x}}_{\text{1}}}} \right)}^{\text{2}}}{\text{ + }}{{\left( {{{\text{y}}_{\text{2}}}{\text{ – }}{{\text{y}}_{\text{1}}}} \right)}^{\text{2}}}} }\]
