The most important rule, in practice, is the Simpson’s Rule, because of its simplicity and accuracy. When more accuracy is required, this rule should be used.
            To find the area  as shown in figure, the base must be divided into an even number of strips of equal width, producing an odd number of ordinates. The length of each ordinate  is accurately measured. The first and the last ordinates are called extreme ordinates; second, fourth, sixth, etc., the even ordinates; and third, fifth, seventh, etc. are odd ordinates.

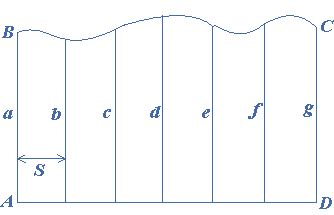
            By Simpson’s Rule, the area is determined as:
                        Area
            Where Sum of the first and the last ordinate
                        Sum of odd ordinates
                        Sum of even ordinates
                        Width of each strip
Note: This rule is applicable only when there will be an even number of strips or odd number of ordinates.

Example:
            Find the area of an irregular figure whose ordinates are, , , , , ,  and  respectively. The width of each strip is m.
Solution:
            Since, the number of ordinates is odd; therefore, we use Simpson’s Rule
                        Area
            Here     m
                       
                       
                       
            Area
                      Square meter.

Example:
            A parabolic piece of card board from root to tipm long. At  equidistant places, the widths are: , , , , , , ,  and m. Find out its area.
Solution:
            Since, the Simpson’s Rule is
                        Area
            Here     m
                       
                       
                       
            Area
                      Square meter.