Trapezoidal Rule

To find the area of the trapezium as shown in the figure, the base $AD$ is divided into equal intervals of width $S$. The ordinates $a,b,c,d,e,f,g$ are accurately measured. The approximation used in this rule is to assume that each strip is equal to the area of a trapezium. Therefore:

Area of a trapezium $= \frac{1}{2}$ (sum of parallel sides) $\times$ (perpendicular distance between the parallel sides)

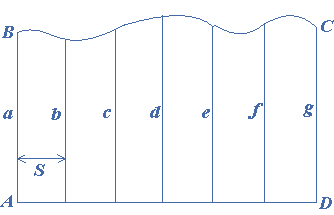
Hence, the first strip's approximate area is $\frac{1}{2}\left( {a + b} \right)S$

For the second strip, the approximate area is $\frac{1}{2}\left( {c + d} \right)S$, and so on.

Therefore, the approximate area of $ABCD$

$= \frac{1}{2}\left( {a + b} \right)S + \frac{1}{2}\left( {b + c} \right)S + \frac{1}{2}\left( {c + d} \right)S + \frac{1}{2}\left( {d + e} \right)S + \frac{1}{2}\left( {e + f} \right)S + \frac{1}{2}\left( {f + g} \right)S$

$= S\left( {\frac{{a + b}}{2} + \frac{{b + c}}{2} + \frac{{c + d}}{2} + \frac{{d + e}}{2} + \frac{{e + f}}{2} + \frac{{f + g}}{2}} \right)$

$= S\left( {\frac{a}{2} + b + c + d + e + f + \frac{g}{2}} \right) = S\left( {\frac{{a + g}}{2} + b + c + d + e + f} \right)$

Area $=$ $($width of interval$)$ $[$sum of first and last ordinate $/2$ + sum of remaining ordinates$]$

 

Example:

Find the area of a cross-section of a river along a line where the depths at equal intervals of $10$m are noted as $0,7,11,15,5,0$m, respectively.

 

Solution:

Width of each strip, $S = 10$m
Ordinates are $= 0,7,11,15,5,0$

Since,

Area $=$ $($width of interval$)$ $[$sum of first and last ordinate $/2$ + sum of remaining ordinates$]$
                                 $= 10\left[ {\frac{{0 + 0}}{2} + 7 + 11 + 15 + 5} \right] = 10 \times 38 = 380$ square meters.

 

Example:

Apply the trapezoidal rule to find the area of a plot of land having the following dimensions:

Ordinates: $2,7,18,38$ and $70$m

Common distance: $33$m

 

Solution:

Given that $a = 2$m, $b = 7$m, $c = 18$m, $d = 38$m, $e = 70$m respectively and $S = 33$m
$\therefore$ by the trapezoidal rule:

Area $= S\left[ {\frac{{a + e}}{2} + \left( {b + c + d} \right)} \right]$
$= 33\left[ {\frac{{2 + 70}}{2} + \left( {7 + 18 + 38} \right)} \right]$
$= 33\left[ {36 + 63} \right] = 33\left( {99} \right) = 3102$ square meters.