|
Ellipse:
An ellipse is a curved line such the sum of the distance of any point in it from two fixed points is constant. In the figure  and  are the two fixed points. The fixed points are called foci. The point  is the center of the ellipse.  is the major axis and  is the minor axis.  and are the semi-axes.
Area of an Ellipse:
The area of a circle is given by the formula , which may be written as  . If a circle is flattened it will take the form of an ellipse and the semi-axes of such an ellipse (like and in given figure) will be the lengthened and shortened radii.
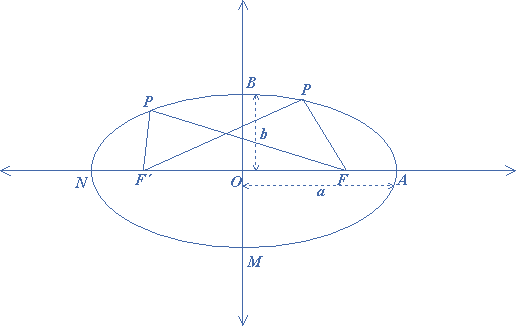
If  stands for and  stands for , it can be proved that the area of the ellipse can be found by substituting  and  in the formula for the area of the circle, which then gives the following formula for the area of an ellipse:
Where  semi-major axis or  major axis.
 semi-minor axis or minor axis.
Example:
Find the radius of a circle equal in area so that of an ellipse whose axes are  cm and  cm.
Solution:
Here , 
 Area of the ellipse 
| 
