Area of a Segment

A segment is a portion of a circle which is cut off by a straight line not passing through the center. The segment smaller than the semi-circle is called the minor segment and the segment larger than the semi-circle is called the major segment.

(a) The area of the minor segment when angle $$\theta $$ and radius $$r$$ are given:

Area of segment $$ = $$ area of sector $$AOBC$$ $$ \pm $$ area of $$\Delta AOB$$
$$ = \frac{1}{2}{r^2}\theta \pm \frac{1}{2}{r^2}\sin \theta $$
$$ = \frac{1}{2}{r^2}(\theta – \sin \theta )$$

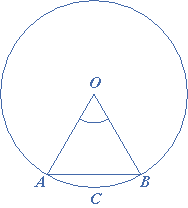
Now the area of the major segment $$ = $$ area of circle $$ – $$ area of the minor segment
$$ = \frac{1}{2}{r^2}(2\pi – \theta + \sin \theta )$$

 

Example:

A chord $$AB$$ of a circle of radius $$15$$cm makes an angle of $${60^ \circ }$$at the center of the circle. Find the area of the major and minor segment.

 

Solution:

 

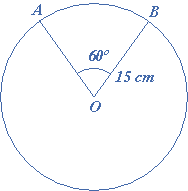
Given that $$\angle AOB = {60^ \circ }$$, radius, $$r = 15$$cm

$$\therefore $$ area of the sector $$OAB$$ $$ = \frac{\theta }{{360}} \times \pi {r^2}$$
$$ = \frac{{60}}{{360}} \times 3.1415 \times 15 \times 15 = 117.75$$ square cm
$$\therefore $$ area of $$\Delta OAB$$ $$ = \frac{1}{2}{r^2}\sin \theta $$
$$ = \frac{1}{2} \times 15 \times 15 \times \sin {60^ \circ } = \frac{{225 \times 1.73}}{4} = 97.31$$ square cm
Area of the minor segment $$ = $$ area of sector $$OAB$$$$ – $$ area of  $$\Delta OAB$$
$$ = 117.75 – 97.31 = 20.44$$ square cm
Area of the circle $$ = \pi {r^2}$$
$$ = 3.1415 \times {(15)^2} = 3.1415 \times 225 = 706.5$$ square cm
Area of the major segment $$ = $$ area of the circle $$ – $$ area of the minor segment
$$ = 706.5 – 20.4 = 686.1$$ square cm.

(b) The area of a segment when the height and length of the chord of the segment are given:

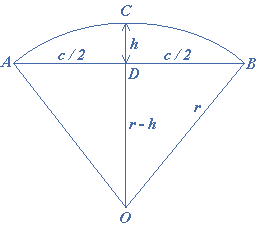
Let $$r = $$ be the radius of the circle
$$h = $$ be the height of the segment
$$c = $$ be the length of the chord

We note that $$ODB$$ is a right triangle; the hypotenuse is $$OB = r$$ and the other two sides are $$OD = r – h$$ and $$BD = c/2$$
$$\therefore $$     by Pythagorean Theorem

$${\left( {\frac{c}{2}} \right)^2} + {\left( {r – h} \right)^2} = {r^2}$$
$${\left( {\frac{c}{2}} \right)^2} + {r^2} – 2rh + {h^2} = {r^2}$$
$${\left( {\frac{c}{2}} \right)^2} – 2rh + {h^2} = 0$$

 

Solving for $$r$$, $$c$$ and $$h$$, we obtain the following formulas:

$$r = \frac{{{{\left( {\frac{c}{2}} \right)}^2} + {h^2}}}{{2h}}$$ — (1)
$$h = r \pm \sqrt {{r^2} – {{\left( {\frac{c}{2}} \right)}^2}} $$ — (2)
$$c = 2\sqrt {h\left( {2r – h} \right)} $$ — (3)

 

Note:
$$r + \sqrt {{r^2} – {{\left( {\frac{c}{2}} \right)}^2}} $$ gives the height of the major segment
$$r – \sqrt {{r^2} – {{\left( {\frac{c}{2}} \right)}^2}} $$ gives the height of the minor segment

 

Many formulas are given for finding the approximate area of a segment. Two of the common methods are:

Method-I: $$A = \frac{{2hc}}{3} + \frac{{{h^2}}}{{2c}} = \frac{h}{{6c}}\left( {3{h^2} + 4{c^2}} \right)$$
Note: If the height of the segment is less $$\frac{1}{{10}}$$ than the radius of the circle, then $$A = \frac{{2hc}}{3}$$.

Method-II: $$A = \frac{{4{h^2}}}{3}\sqrt {\frac{{2r}}{h} – 0.608} $$

 

Example:

If the chord of the segment of a circle is $$66$$ cm and the height of the segment is $$10$$ cm, find the radius of the circle.

 

Solution:

Given that, $$c = 66$$cm, $$h = 10$$cm
$$\therefore $$     $$r = \frac{{{{\left( {\frac{c}{2}} \right)}^2} + {h^2}}}{{2h}}$$
$$ = \frac{{{{(33)}^2} + {{(10)}^2}}}{{2 \times 10}} = \frac{{1089 + 100}}{{20}} = 59.45$$cm

 

Example:

Find the area of the segment whose chord is $$10$$ cm and whose height is $$1.5$$ cm.

 

Solution:

Given that $$h = 1.5$$cm, $$c = 10$$cm
$$\therefore $$     $$A = \frac{{2hc}}{3} + \frac{{{h^2}}}{{2c}}$$
$$ = \frac{2}{3}(1.5)(10) + \frac{{{{(1.5)}^2}}}{{2 \times 1}} = 10.17$$ square cm.