Parametric Equations of a Circle

Draw a circle with centre at $O\left( {0,0} \right)$ and with a radius equal to $r$ which is the fixed distance from the centre of the circle. Now let $P\left( {x,y} \right)$ be any point of the circle as shown in the diagram. Draw a perpendicular from point $P\left( {x,y} \right)$ on the X-axis, meeting at the point $M$. Consider the triangle $OMP$ which is a right angle triangle where $OM$ is the base of the right triangle and $MP$ is the perpendicular of the triangle.

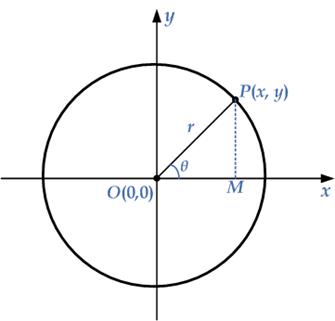
From the basic ratios of trigonometry,

$$\begin{gathered} \frac{{OM}}{{OP}} = \cos \theta \\ \Rightarrow OM = OP\cos \theta \,\,\,{\text{ - - - }}\left( {\text{i}} \right) \\ \frac{{MP}}{{OP}} = \sin \theta \\ \Rightarrow MP = OP\sin \theta \,\,\,{\text{ - - - }}\left( {{\text{ii}}} \right) \\ \end{gathered}$$

Since $OM = x$, $MP = y$, $OP = r$, putting these values in equation (i) and (ii) we get the following equations:

$$\begin{gathered} x = r\cos \theta \\ y = r\sin \theta \\ \end{gathered}$$

These equations are the called the parametric equations of a circle.

Example: Show that the parametric equations $x = 5\cos t$ and $y = 5\sin t$ represent the equation of circle ${x^2} + {y^2} = 25$.

Solution: We have been given parametric equations,

$$\begin{gathered} x = 5\cos t\,\,\, - - - \left( i \right) \\ y = 5\sin t\,\,\, - - - \left( {ii} \right) \\ \end{gathered}$$

Now squaring and adding equation (i) and (ii), we get

$$\begin{gathered} {x^2} + {y^2} = {\left( {5\cos t} \right)^2} + {\left( {5\sin t} \right)^2} \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 25{\cos ^2}t + 25{\sin ^2}t \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 25\left( {{{\cos }^2}t + {{\sin }^2}t} \right) \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 25\left( 1 \right) \\ \end{gathered}$$

Hence ${x^2} + {y^2} = 25$ is the required equation of the circle.