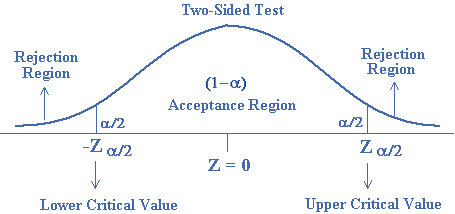
Two-Tailed Test
When the rejection region is taken on both ends of the sampling distribution, the test is called a two-sided test or two-tailed test. When we are using a two-sided test, half of the rejection region equal to $$\alpha /2$$ is taken on the right side and the other half equal to $$\alpha /2$$ is taken on the left side of the sampling distribution. Suppose the sampling distribution of the statistic is a normal distribution and we have to test the hypothesis $${H_o}:\theta = {\theta _o}$$ against the alternative hypothesis $${H_1}:\theta \ne {\theta _o}$$ which is two-sided. $${H_o}$$ is rejected when the calculated value of $$Z$$ is greater than $${Z_{\alpha /2}}$$ or it is less than $$ – {Z_{\alpha /2}}$$.
Thus the critical region is $$Z > {Z_{\alpha /2}}$$ or$$Z <- {Z_{\alpha /2}}$$, and it can also be written as $$ – {Z_{\alpha /2}} < Z < {Z_{\alpha /2}}$$.