Intersection of a Line and Hyperbola

A line $$y = mx + c$$ intersects a hyperbola $$\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1$$ at two points maximum and the condition for this intersection is $${c^2} > {a^2}{m^2} – {b^2}$$.

Consider the equation of a line is represented by

\[y = mx + c\,\,\,{\text{ – – – }}\left( {\text{i}} \right)\]

Consider the standard equation of a hyperbola with vertex at origin $$\left( {0,0} \right)$$ can be written as

\[\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\,\,\,{\text{ – – – }}\left( {{\text{ii}}} \right)\]

To find the point of intersection of straight line (i) and the given hyperbola (ii), we have to solve equation (i) and equation (ii) by the method of simultaneously equations. Using the case when one equation is in quadratic from and the other one is in linear form, we put the value of $$y$$ from equation (i) into the equation of a hyperbola (ii), i.e. the equation of a hyperbola becomes:

\[\begin{gathered} \frac{{{x^2}}}{{{a^2}}} – \frac{{{{\left( {mx + c} \right)}^2}}}{{{b^2}}} = 1 \\ \Rightarrow \frac{{{b^2}{x^2} – {a^2}{{\left( {mx + c} \right)}^2}}}{{{a^2}{b^2}}} = 1 \\ \Rightarrow {b^2}{x^2} – {a^2}{\left( {mx + c} \right)^2} = {a^2}{b^2} \\ \Rightarrow {b^2}{x^2} – {a^2}\left( {{m^2}{x^2} + 2mcx + {c^2}} \right) = {a^2}{b^2} \\ \Rightarrow {b^2}{x^2} – {a^2}{m^2}{x^2} – 2{a^2}mcx – {a^2}{c^2} – {a^2}{b^2} = 0 \\ \Rightarrow \left( {{a^2}{m^2} – {b^2}} \right){x^2} + 2{a^2}mcx + {a^2}\left( {{b^2} – {c^2}} \right) = 0\,\,\,{\text{ – – – }}\left( {{\text{iii}}} \right) \\ \end{gathered} \]

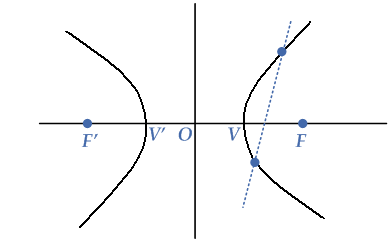
Since equation (iii) is a quadratic equation in $$x$$ it can have at most two roots. This shows that the line (i) can intersect the hyperbola (ii) at two points maximum. This is also clear from the given diagram.

Equation (iii) will have two real roots if

\[\begin{gathered} {\text{Discriminant > 0}} \\ \Rightarrow {\left( {2{a^2}mc} \right)^2} – 4\left( {{a^2}{m^2} – {b^2}} \right){a^2}\left( {{b^2} + {c^2}} \right) > 0 \\ \Rightarrow 4{a^4}{m^2}{c^2} – 4{a^2}\left( {{a^2}{m^2} – {b^2}} \right)\left( {{b^2} + {c^2}} \right) > 0 \\ \Rightarrow {a^2}{m^2}{c^2} – \left( {{a^2}{m^2} + {b^2}} \right)\left( {{c^2} – {b^2}} \right) > 0 \\ \Rightarrow – {a^2}{m^2} + {b^2} + {c^2} > 0 \\ \Rightarrow \boxed{{c^2} > {a^2}{m^2} – {b^2}} \\ \end{gathered} \]