Curved Surface Area of a Cone

If a perpendicular cut is made from a point on the circumference of the base to the vertex and the cone is opened up, a sector of a circle with radius $$l$$ is produced. Since the circumference of the base of the cone is $$2\pi r$$, therefore the arc length of the sector of the circle is $$2\pi r$$.

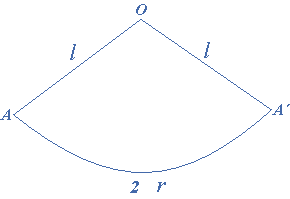
\[\begin{gathered} {\text{Curved surface area}} = {\text{Area of sector }}OAA’ \\ {\text{Curved surface area}} = \left( {\frac{{{\text{Arc length of sector}}}}{{{\text{Circumference of circle}}}}} \right) \times {\text{Area of circle}} \\ {\text{Curved surface area}} = \frac{{2\pi r}}{{2\pi l}} \times \pi {l^2} = \pi rl \\ \end{gathered} \]

            Where
$$l = $$ slant height of the cone
$$r = $$ radius of the base of the cone

Total Surface Area

The total surface area $$ = $$area of curved surface $$ + $$area of base
$$\therefore $$     $$S = \pi rl + \pi {r^2} = \pi r\left( {l + r} \right)$$

Rule:

1. The curved surface area of a right circular cone equals the perimeter of the base times one-half slant height.
2. The total surface area equals the curved surface area of the base.

Example:

The slant height of a conical tomb is $$10.5$$ m. If its diameter is $$16.8$$ m, find the cost of cleaning it at $2 per cubic meter and also the cost of whitewashing the curved surface at $$50$$ cents per square meter.

Solution:
            Now, slant height,       $$l = 10.5$$ m
Perpendicular height $$h = \sqrt {{{\left( {10.5} \right)}^2} – {{\left( {8.4} \right)}^2}} = 6.3$$ m   (as $$h = \sqrt {{l^2} – {r^2}} $$)
Volume of the conical tomb $$ = \frac{1}{3}\pi {r^2}h$$
$$ = \frac{1}{3} \times \frac{{22}}{7} \times 8.4 \times 8.4 \times 6.3$$
$$ = 465.7$$ cubic meters
Cost of construction             $$ = 465.7 \times 2 = 931.39$$
Curved surface                     $$ = \pi rl = \frac{{22}}{7} \times 8.4 \times 10.6 = 277.2$$ square meters
Cost of white washing                      $$ = 277.2 \times \frac{{50}}{{100}} = 138.60$$ dollars