The Area of a Rhombus
A rhombus is a quadrilateral having all sides with unequal diagonals which bisect each other.
Note: If a square is pressed from two opposite corners, a rhombus is formed.
Let $$ABCD$$ be a rhombus, then its area can be evaluated in two ways.
(1) When one side and the included angle is given:
Let one side be equal to $$a$$ with includes angle $$\theta $$. Since the diagonal $$AC$$ divides the rhombus into two equal triangles, therefore

The area of the rhombus $$ = 2 \times {\text{area of }}\Delta ABC$$.
The area of the rhombus $$ = 2\left( {\frac{1}{2}a \times a \times \sin \theta } \right) = 2\left( {\frac{1}{2}{a^2}} \right)\sin \theta = {a^2}\sin \theta $$.
The area of the rhombus $$ = {({\text{one side}})^2}\sin \theta $$.
(2) When two diagonal are given:
Let $$d$$ and $$d’$$ be the length of the diagonals $$AC$$ and $$BD$$ respectively, and since the rhombus is divided into four equal triangles, therefore
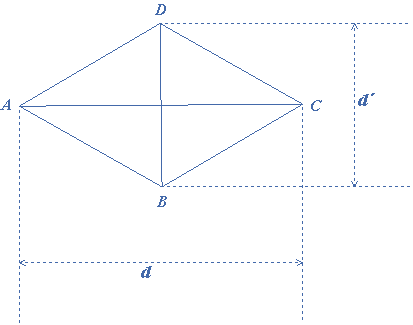
The area of the rhombus $$ = 4 \times \frac{1}{2} \times \frac{{BD}}{2} \times \frac{{CA}}{2} = 4 \times \frac{{BD \times CA}}{8} = \frac{{BD \times CA}}{2}$$.
The area of the rhombus $$ = \frac{{AC \times BD}}{2} = \frac{{d \times d’}}{2}$$.
The area of the rhombus $$ = \frac{{{\text{Product of two diagonals}}}}{2}$$.
Example:
The length of each side of a rhombus is $$120$$ cm and two of its opposite angles are $$60^\circ $$ each. Find the area.
Solution:
Given that each side $$a = 120$$ and $$\theta = 60^\circ $$,
the area of the rhombus $$ = {({\text{side}})^2} \times \sin \theta $$.
The area of the rhombus $$ = 120 \times 120 \times \sin 60^\circ = 120 \times 120 \times 0.866 = 12470.4$$ square cm.
Example:
The diagonals of a rhombus are $$40$$ m and $$30$$ m. Find its area.
Solution:
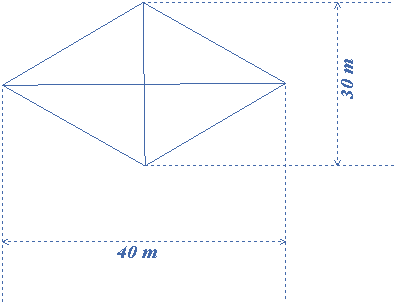
Given that the diagonals are $$d = 40$$ m and $$d’ = 30$$ m,
the area of the rhombus $$ = \frac{{d \times d’}}{2} = \frac{{40 \times 30}}{2} = 600$$ square m.
