|
Consider the first figure and suppose that one semi-circle is cut form the centre nearly to the circumference in each direction. Then the semi-circle is spread out as in second figure. The length  is the length half circumference of the circle.
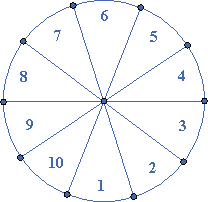
Suppose that the other half of the circle is cut in the same way and fitted into the first, as shown by the dashes in second figure. It is evident that if we make a large number of cuts, the figure formed will approximate a rectangle whose length is equal to one-half the circumference and whose width is equal to the radius. We note that the rectangle is  or  and this rectangle has the same area as the circle.
Rule: The area of a circle equals  times the square of the radius or the area of a circle equal one-fourth  times the square of the diameter.
If  area,  circumference,  diameter,  radius, then
 (if radius is given)
 (if diameter is given)
 (if circumference and radius are given)
Example:
A reinforced concrete beam is to have a total area of steel of  square cm. How many bars must be used if they are to be  cm, diameter?
Solution:
Given that, total area of reinforced concrete beam  Square cm --- (1)
 Area of the circle of  cm. diameter 
 Square cm --- (2)
 Number of bars  (approx)
Example:
A paper is in the form of a rectangle , where  cm and  cm. A semi-circular portion with  as diameter is cut off. Find the area of the remaining paper.
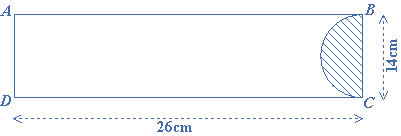
Solution:
Area of rectangle  Square cm
Area of semi-circle 
 Square cm
 Required area of the remaining paper  Square cm.
| 
