Some Basic Types and Results of Triangles
1. An angle whose measurement is of $${90^ \circ }$$ is called a RIGHT ANGLE.
2. An angle whose measurement is greater than $${90^ \circ }$$ is called an OBTUSE ANGLE.
3. An angle whose measurement is less than $${90^ \circ }$$ is called an ACUTE ANGLE.
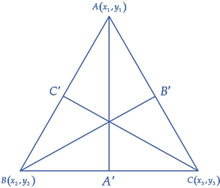
4. If $${A^{‘}}$$, $${B^{‘}}$$ and $${C^{‘}}$$ are the midpoints of the sides of $$\Delta ABC$$, then $$\overline {A{A^{‘}}} $$, $$\overline {B{B^{‘}}} $$ and $$\overline {C{C^{‘}}} $$ are called the medians of the triangles, and the medians of a triangle are concurrent at the point $$\left( {\frac{{{x_1} + {x_2} + {x_3}}}{2},\frac{{{y_1} + {y_2} + {y_3}}}{2}} \right)$$
5. If $$\overline {AE} $$, $$\overline {BF} $$ and $$\overline {CG} $$ are the perpendiculars from $$A$$, $$B$$, $$C$$ to the sides $$(BC)$$, $$(AC)$$ and $$(AB)$$ of $$\Delta ABC$$ respectively, then $$\overline {AE} $$, $$\overline {BF} $$ and $$\overline {CG} $$ are called the ALTITUDES OF THE TRIANGLE.

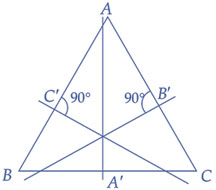
6. The lines passing through the mid points of the sides of $$\Delta $$, and perpendicular to the respective sides, are called the RIGHT BISECTORS OF THE TRIANGLE.
7. Angle bisectors of a triangle are concurrent at $$G = \left( {\frac{{a{x_1} + b{x_2} + c{x_3}}}{{a + b + c}},\frac{{a{y_1} + b{y_2} + c{y_3}}}{{a + b + c}}} \right)$$.

8. A triangle whose one angle is $${90^ \circ }$$ is called a RIGHT ANGLED TRIANGLE.
9. A triangle whose sides are of equal length is called an EQUILATERAL TRIANGLE.
10. A triangle whose two sides or two angles are equal measurements is called an ISOSCELES TRIANGLE.
11. If $$\alpha $$, $$\beta $$ and $$\gamma $$ are the internal angles of a triangle, then $$\alpha + \beta + \gamma = {180^ \circ }$$
