|
If a sphere is placed in a cylinder of the same diameter and with an altitude equal to the diameter, and the vacant spaces are filled with sand, the sand will be found to fill exactly one-third of the cylinder after the sphere is removed.
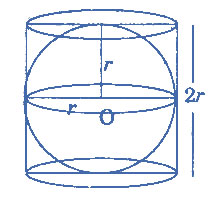
Therefore, a sphere is equal to two-third of a cylinder of the same diameter and height.
Here the volume of the cylinder 
 The volume of the sphere 
Summary:
- Volume of a sphere
 or  , where  is the radius and  is the diameter of the sphere.
- Volume of a hemisphere
 |
