Translation of Axes

If in the plane with the given $$X$$ and $$Y$$ axes new coordinate axes are chosen parallel to the given ones, we say that there has been a translation of axes in the plane.

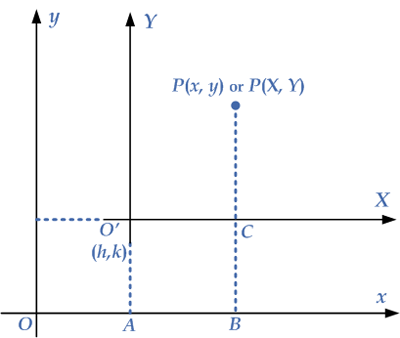
Let $$P\left( {x,y} \right)$$ be any point in the $$XY$$-plane. Let $$O’\left( {h,k} \right)$$ be the fixed point in the $$XY$$- plane. We draw two perpendicular axes through $$O’$$: the $$X$$-axis is parallel to the $$x$$-axis and the $$Y$$-axis parallel to the $$y$$-axis, as shown in the given diagram. In fact, $$O’$$ is the origin of the new $$XY$$-plane. The point $$P$$ has the coordinates $$\left( {X,Y} \right)$$ with respect to the $$XY$$-plane.

Now
\[\begin{gathered} X = O’C = AB = OB – OA = x – h\,\,\,\,\,\,\,\because X = O’C,\,\,OB = x,\,\,OA = h \\ Y = CP = BP – BC = y – k\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\because Y = CP,\,\,BP = y,\,\,BC = k \\ \end{gathered} \]

The equations $$X = x – h$$, $$Y = y – k$$ are called transformation equations and are used to find the coordinates of a point with respect to the new coordinate system, the $$XY$$-system. Thus, the point $$P\left( {x,y} \right)$$ with respect to the XY-plane is $$P\left( {x – h,y – k} \right)$$.

Conversely, if the coordinates of a point with respect to the $$XY$$-system are given, then the coordinates with respect to the original system can be determined by the equations $$x = X + h$$, $$y = Y + k$$.

Example 1: Let $$P\left( {8,3} \right)$$ and $$O’\left( {2, – 5} \right)$$ be two points in the XY-coordinates system. Find the XY-coordinates of $$P$$ referring to the translated axes $$O’X$$ and $$O’Y$$.

Solution: Here $$x = 8,\,\,y = 3$$ and $$h = 2,\,\,k = – 5$$. The coordinates of $$P$$ referring to the new $$XY$$-coordinates system are
\[\left( {x – h,y – k} \right) = \left( {8 – 2,3 – \left( { – 5} \right)} \right) = \left( {6,8} \right)\]

Example 2: Let $$P\left( {3,4} \right)$$ be a point referring to the $$XY$$-coordinate system translated thorough $$O’\left( {5,6} \right)$$. Find the coordinates of $$P$$ referring to the original coordinate system,  the $$xy$$-system.

Solution: Here $$X = 3,\,\,Y = 4$$ and $$h = 5,\,\,k = 6$$. The coordinates of $$P$$ referring to the new XY-coordinates system are
\[\left( {X + h,Y + k} \right) = \left( {3 + 5,4 + 6} \right) = \left( {8,10} \right)\]