The Midpoint of the Hypotenuse is the Circumcenter of the Right Triangle

The midpoint of the hypotenuse of a right triangle is the circumcenter of the triangle.

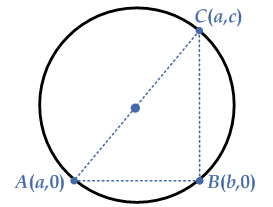
Consider the equation of the circle in general form is given by
\[{x^2} + {y^2} + 2gx + 2fy + c = 0\,\,\,\,{\text{ – – – }}\left( {\text{i}} \right)\]

Let $$A\left( {a,0} \right)$$, $$B\left( {b,0} \right)$$ and $$C\left( {b,c} \right)$$ be any three points on the given circle.

For the point $$A\left( {a,0} \right)$$, since the point $$A$$ is on the circle then the equation of the circle becomes
\[\begin{gathered} {\left( a \right)^2} + {\left( 0 \right)^2} + 2g\left( a \right) + 2f\left( 0 \right) + c = 0 \\ {a^2} + 2ag + c = 0\,\,\,\,{\text{ – – – }}\left( {{\text{ii}}} \right) \\ \end{gathered} \]

For the point $$B\left( {b,0} \right)$$, since the point $$B$$ is on the circle then the equation of the circle becomes
\[\begin{gathered} {\left( b \right)^2} + {\left( 0 \right)^2} + 2g\left( b \right) + 2f\left( 0 \right) + c = 0 \\ {b^2} + 2bg + c = 0\,\,\,\,{\text{ – – – }}\left( {{\text{iii}}} \right) \\ \end{gathered} \]

For the point $$C\left( {b,c} \right)$$, since the point $$C$$ is on the circle then the equation of the circle becomes
\[\begin{gathered} {\left( b \right)^2} + {\left( c \right)^2} + 2g\left( b \right) + 2f\left( c \right) + c = 0 \\ {b^2} + {c^2} + 2bg + 2cf + c = 0\,\,\,\,{\text{ – – – }}\left( {{\text{iv}}} \right) \\ \end{gathered} \]

Now solving equation (iv) and equation (iii), we get the value
\[\begin{gathered} 2cf = – {c^2} \\ f = – \frac{{{c^2}}}{{2c}} \Rightarrow f = – \frac{c}{2} \Rightarrow – f = \frac{c}{2} \\ \end{gathered} \]

Solving equation (ii) and equation (iii), we get the value
\[\begin{gathered} \left( {{a^2} – {b^2}} \right) + \left( {2a – 2b} \right)g = 0 \\ \Rightarrow 2\left( {a – b} \right)g = – \left( {{a^2} – {b^2}} \right) \\ \Rightarrow g = \frac{{ – \left( {a – b} \right)\left( {a + b} \right)}}{{2\left( {a – b} \right)}} \\ \Rightarrow – g = \frac{{a + b}}{2} \\ \end{gathered} \]

The center of the circle is given by
\[\left( { – g, – f} \right) = \left( {\frac{{a + b}}{2},\frac{c}{2}} \right)\]

Now the midpoint of the hypotenuse is given as
\[\begin{gathered} AC = \left( {\frac{{{x_1} + {x_2}}}{2},\frac{{{y_1} + {y_2}}}{2}} \right) \\ AC = \left( {\frac{{a + b}}{2},\frac{{0 + c}}{2}} \right) = \left( {\frac{{a + b}}{2},\frac{c}{2}} \right) \\ \end{gathered} \]

Thus, the midpoint of the hypotenuse is equal to the center of the circle.