The Medians of a Triangle are Concurrent
The medians of any triangle are concurrent and that the point of concurrency divides each one of them in the ratio 2:1.
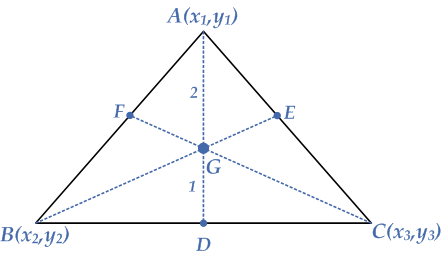
Consider the triangle $$ABC$$ as shown in the diagram and suppose that $$A\left( {{x_1},{y_1}} \right)$$, $$B\left( {{x_2},{y_2}} \right)$$ and $$C\left( {{x_3},{y_3}} \right)$$ are the vertices of the given triangle $$ABC$$. As we know, the median is defined as the line segment joining the vertex of the triangle to the midpoint to the opposite side of the triangle.
Now suppose that $$D$$, $$E$$ and $$F$$ are the midpoints of the sides of the triangle $$ABC$$, so these midpoints can be calculated using the midpoint formula as follows:
\[{\text{Midpoint}} = \left( {\frac{{{x_1} + {x_2}}}{2},\frac{{{y_1} + {y_2}}}{2}} \right)\]
The midpoint of side $$BC$$ is $$D = \left( {\frac{{{x_2} + {x_3}}}{2},\frac{{{y_2} + {y_3}}}{2}} \right)$$
The midpoint of side $$AC$$ is $$E = \left( {\frac{{{x_1} + {x_3}}}{2},\frac{{{y_1} + {y_3}}}{2}} \right)$$
The midpoint of side $$AB$$ is $$F = \left( {\frac{{{x_1} + {x_2}}}{2},\frac{{{y_1} + {y_2}}}{2}} \right)$$
Consider $$G$$ is the point intersection of the three medians of the triangle $$ABC$$.
First we find the coordinates of the point $$G$$ with respect to the median $$AD$$, since the point $$G$$ divides the median $$AD$$ in the ratio $$2:1$$, i.e. $${k_1}:{k_2} = 2:1$$. We find the point $$G$$ using the division formula or ratio formula (internal division).
Let $$\left( {{x_1},{y_1}} \right) = \left( {{x_1},{y_1}} \right)$$ and $$\left( {{x_2},{y_2}} \right) = \left( {\frac{{{x_2} + {x_3}}}{2},\frac{{{y_2} + {y_3}}}{2}} \right)$$
\[\begin{gathered} G = \left( {\frac{{{k_2}{x_1} + {k_1}{x_2}}}{{{k_1} + {k_2}}},\frac{{{k_2}{y_1} + {k_1}{y_2}}}{{{k_1} + {k_2}}}} \right) \\ G = \left( {\frac{{\left( 1 \right){x_1} + \left( 2 \right)\left( {\frac{{{x_2} + {x_3}}}{2}} \right)}}{{1 + 2}},\frac{{\left( 1 \right){y_1} + \left( 2 \right)\left( {\frac{{{y_2} + {y_3}}}{2}} \right)}}{{1 + 2}}} \right) \\ G = \left( {\frac{{{x_1} + {x_2} + {x_3}}}{3},\frac{{{y_1} + {y_2} + {y_3}}}{3}} \right) \\ \end{gathered} \]
Second we find the coordinates of the point $$G$$ with respect to the median $$BE$$, since the point $$G$$ divides the median $$BE$$ in the ratio $$2:1$$, i.e. $${k_1}:{k_2} = 2:1$$. We find the point $$G$$ using the division formula or ratio formula (internal division).
Let $$\left( {{x_1},{y_1}} \right) = \left( {{x_2},{y_2}} \right)$$ and $$\left( {{x_2},{y_2}} \right) = \left( {\frac{{{x_1} + {x_3}}}{2},\frac{{{y_1} + {y_3}}}{2}} \right)$$
\[\begin{gathered} G = \left( {\frac{{{k_2}{x_1} + {k_1}{x_2}}}{{{k_1} + {k_2}}},\frac{{{k_2}{y_1} + {k_1}{y_2}}}{{{k_1} + {k_2}}}} \right) \\ G = \left( {\frac{{\left( 1 \right){x_2} + \left( 2 \right)\left( {\frac{{{x_1} + {x_3}}}{2}} \right)}}{{1 + 2}},\frac{{\left( 1 \right){y_2} + \left( 2 \right)\left( {\frac{{{y_1} + {y_3}}}{2}} \right)}}{{1 + 2}}} \right) \\ G = \left( {\frac{{{x_1} + {x_2} + {x_3}}}{3},\frac{{{y_1} + {y_2} + {y_3}}}{3}} \right) \\ \end{gathered} \]
Similarly, the coordinates of $$G$$ with respect to $$CF$$.
Hence, the medians of the triangle are concurrent and the point of concurrency is
\[G = \left( {\frac{{{x_1} + {x_2} + {x_3}}}{3},\frac{{{y_1} + {y_2} + {y_3}}}{3}} \right)\]
