Line Touching Circle at One Point
Consider the equation of a circle with center at origin $$\left( {0,0} \right)$$ and radius $$r$$. Then the equation of this circle is written as
\[{x^2} + {y^2} = {r^2}\,\,\,{\text{ – – – }}\left( {\text{i}} \right)\]
Now the equation of a line is represented by
\[y = mx + c\,\,\,{\text{ – – – }}\left( {{\text{ii}}} \right)\]
To find the point where the line (ii) touches the circle (i), we use the method of solving simultaneous equations in which one equation is in quadratic and the other is in linear form. So we take the value of $$y$$ from equation (ii) and put this value into equation (i), i.e. the equation of s circle as follows:
\[\begin{gathered} {x^2} + {\left( {mx + c} \right)^2} = {r^2} \\ \Rightarrow {x^2} + {m^2}{x^2} + 2mcx + {c^2} = {r^2} \\ \Rightarrow \left( {1 + {m^2}} \right){x^2} + 2mcx + {c^2} – {r^2} = 0\,\,\,{\text{ – – – }}\left( {{\text{iii}}} \right) \\ \end{gathered} \]
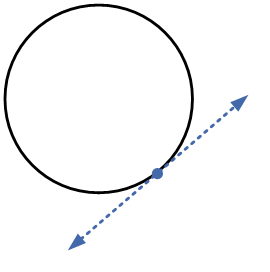
Since equation (iii) is a quadratic equation in $$x$$, we compare this equation with the standard quadratic equation $$a{x^2} + bx + c = 0$$ to obtain the coefficients of $$a,b$$ and $$c$$. We use these values in the discriminant, i.e. $${b^2} – 4ac$$.
\[\begin{gathered} {b^2} – 4ac = {\left( {2mc} \right)^2} – 4\left( {1 + {m^2}} \right)\left( {{c^2} – {r^2}} \right) \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 4{m^2}{c^2} – 4\left( {{c^2} + {m^2}{c^2} – {r^2} – {m^2}{r^2}} \right) \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 4{m^2}{c^2} – 4{c^2} – 4{m^2}{c^2} + 4{r^2} + 4{m^2}{r^2} \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = – 4{c^2} + 4{r^2} + 4{m^2}{r^2} \\ \end{gathered} \]
If the discriminant is equal to zero i.e. $${b^2} – 4ac = 0$$, then equation (iii) will have equal roots and the line will intersect the circle at one point, i.e. it will be a tangent to the circle as shown in the given diagram.
Thus the line is a tangent to the circle if:
\[\begin{gathered} – 4{c^2} + 4{r^2} + 4{m^2}{r^2} = 0 \\ \Rightarrow 4{r^2} + 4{m^2}{r^2} = 4{c^2} \\ \Rightarrow {c^2} = {r^2} + {m^2}{r^2} \\ \Rightarrow c = \pm r\sqrt {\left( {1 + {m^2}} \right)} \,\,\,{\text{ – – – }}\left( {{\text{iv}}} \right) \\ \end{gathered} \]
This is the condition for a line (ii) to be a tangent to a circle (i). Putting these values of $$c$$ into (ii), we have the tangents to the circle. Thus, the tangents to the circle are
\[y = mx \pm r\sqrt {1 = {m^2}} \,\,\,{\text{ – – – }}\left( {\text{v}} \right)\]
NOTE:
(1) The condition (iv) is valid just for a circle whose center is origin, so for a circle with an arbitrary center this condition is not valid.
(2) The lines (v) are tangents to a circle whose center is origin, so for a circle with an arbitrary center these lines may not be the valid.
