Line Intersecting Circle at Two Points

Consider the equation of circle with centre at origin $$\left( {0,0} \right)$$ and radius $$r$$. Then the equation of this circle is written as

\[{x^2} + {y^2} = {r^2}\,\,\,{\text{ – – – }}\left( {\text{i}} \right)\]

Now the equation of a line is represented by

\[y = mx + c\,\,\,{\text{ – – – }}\left( {{\text{ii}}} \right)\]

To find the point of intersection of the line (ii) and the circle (i), using the method of solving simultaneous equations in which one equation is in quadratic and the other is in linear form, take value of $$y$$ from equation (ii) and put this value in equation (i) i.e. the equation of a circle as follows:

\[\begin{gathered} {x^2} + {\left( {mx + c} \right)^2} = {r^2} \\ \Rightarrow {x^2} + {m^2}{x^2} + 2mcx + {c^2} = {r^2} \\ \Rightarrow \left( {1 + {m^2}} \right){x^2} + 2mcx + {c^2} – {r^2} = 0\,\,\,{\text{ – – – }}\left( {{\text{iii}}} \right) \\ \end{gathered} \]

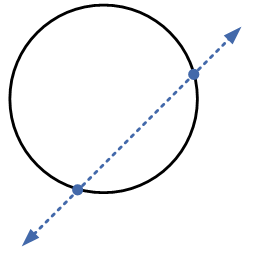
Since equation (iii) is a quadratic equation in $$x$$, we can solve this quadratic equation either by completing the square method or by using the quadratic formula and can have the most roots, i.e. values of $$x$$, and put the values of $$x$$ into equation (ii) to get the values of $$y$$ and obtain two points. These points are the intersection of the line with the circle, i.e. the line (ii) can intersect the circle (i) at two points at the most, which is clear from the given diagram.