A cone is a solid figure generated by a line, one end of which is fixed and the other end describe a closed curve in a plane.
            A circular cone is a solid figure whose base is a circle and whose lateral surface area (i.e. curved surface area) tapers uniformly to a point: which is called the vertex or apex. The axis of the cone is a straight line drawn from the vertex to the center of the base.

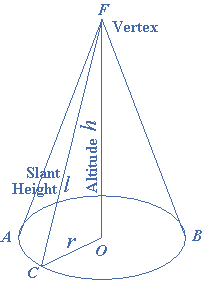
            A right circular cone is a cone whose base is a circle and whose axis is perpendicular to the base. Such a cone can also be described as solid formed by a right triangle rotated about one of its sides as an axis; it may, therefore, be called a cone of revolution. Altitude of a cone is the perpendicular line from the vertex to the base. (as shown in the figure).
            The slant height is the length of a straight line drawn from the vertex to the circumference of the base (as shown in the figure). If is any point on the circle (base of the cone), we obtain by Pythagorean Theorem,
                       
                         
                             
            Where
                         , being slant height of the cone
                          altitude of the cone
                        , radius of the base of the cone
            A pyramid with a circular base is given the special name of cone i.e., a cone may be considered the limiting case of a pyramid when the number of sides of the base polygon increases indefinitely.