The Intercepts Form of a Line
If $$a$$ and $$b$$ are non-zero $$X$$ and $$Y$$ intercepts of a line $$l$$, then its equation is of the form
\[\frac{x}{a} + \frac{y}{b} = 1\]
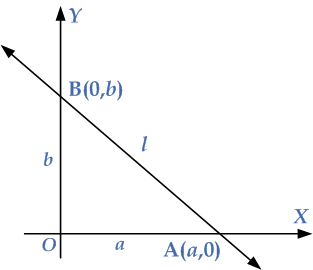
Since $$a$$ is an $$X$$-intercept of the line $$l$$, and as we know that if any point lies on the $$X$$-axis its value of $$Y$$ is equal to zero, it passes through the point $$A\left( {a,0} \right)$$. Also if $$b$$ is the $$Y$$-intercept of the line $$l$$, and we know that any point that lies on the $$Y$$-axis has a value of $$X$$ equal to zero, it passes through the point $$B\left( {0,b} \right)$$ as shown in the given diagram.
Now to prove the intercepts form of a line, use the formula for the two points form of a straight line as given by
\[\frac{{y – {y_1}}}{{{y_2} – {y_1}}} = \frac{{x – {x_1}}}{{{x_2} – {x_1}}}\]
Take $$A\left( {a,0} \right) = \left( {{x_1},{y_1}} \right)$$ and $$B\left( {0,b} \right) = \left( {{x_2},{y_2}} \right)$$, and put these values in the above formula:
\[\begin{gathered} \Rightarrow \frac{{y – 0}}{{b – 0}} = \frac{{x – a}}{{0 – a}} \\ \Rightarrow \frac{y}{b} = \frac{x}{{ – a}} – \frac{a}{{ – a}} \\ \end{gathered} \]
\[ \Rightarrow \boxed{\frac{x}{a} + \frac{y}{b} = 1}\]
This is the required equation of a straight line in intercepts form.
Example: Find the equation of a straight line with $$X$$-intercept $$A\left( {3,0} \right)$$ and $$Y$$-intercept $$B\left( {0,2} \right)$$.
From the above information we know the $$X$$-intercept is $$a = 3$$ and the $$Y$$-intercept is $$b = 2$$. Now we put all these values in the formula of the intercepts form as given:
\[\begin{gathered} \frac{x}{a} + \frac{y}{b} = 1 \\ \Rightarrow \frac{x}{3} + \frac{y}{2} = 1 \\ \Rightarrow 2x + 3y = 6 \\ \Rightarrow 2x + 3y – 6 = 0 \\ \end{gathered} \]
This is the required equation of a straight line.
