Equation of a Circle with Endpoints of Diameter

Let $$A\left( {{x_1},{y_1}} \right)$$ and $$B\left( {{x_2},{y_2}} \right)$$ be the end points of the diameter of the circle as shown in the diagram.

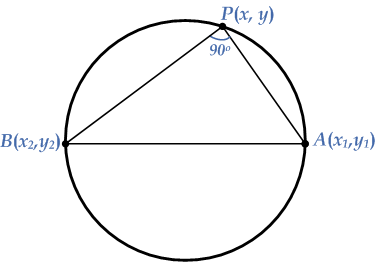
Let $$P\left( {x,y} \right)$$ be any point of the circle. Connecting the points $$A$$ and $$B$$ with the point $$P$$ makes an angle $${90^ \circ }$$ between them. First we find the slopes of the lines $$PA$$ and $$PB$$ as:

Slope of the line $$PA = \frac{{y – {y_1}}}{{x – {x_1}}}$$
Slope of the line $$PB = \frac{{y – {y_2}}}{{x – {x_2}}}$$

Since $$m\angle APB = {90^ \circ }$$, the lines $$PA$$ and $$PB$$ are perpendicular to each other. Therefore, the product of their slopes is $$ – 1$$. i.e.:

\[\begin{gathered} \frac{{y – {y_1}}}{{x – {x_1}}} \times \frac{{y – {y_2}}}{{x – {x_2}}} = – 1 \\ \Rightarrow \frac{{\left( {y – {y_1}} \right)\left( {y – {y_2}} \right)}}{{\left( {x – {x_1}} \right)\left( {x – {x_2}} \right)}} = – 1 \\ \Rightarrow \left( {y – {y_1}} \right)\left( {y – {y_2}} \right) = – \left( {x – {x_1}} \right)\left( {x – {x_2}} \right) \\ \end{gathered} \]
\[ \Rightarrow \boxed{\left( {x – {x_1}} \right)\left( {x – {x_2}} \right) + \left( {y – {y_1}} \right)\left( {y – {y_2}} \right) = 0}\]

This is the equation of the circle through the extremities (ends) of its diameter. In order to find the centre and radius of this circle, we simplify the above equation of a circle as follows:

\[\begin{gathered} {x^2} – {x_1}x – {x_2}x + {x_1}{x_2} + {y^2} – {y_1}y – {y_2}y + {y_1}{y_2} = 0 \\ \Rightarrow {x^2} + {y^2} – \left( {{x_1} + {x_2}} \right)x – \left( {{y_1} + {y_2}} \right)y + {x_1}{x_2} + {y_1}{y_2} = 0 \\ \end{gathered} \]

Comparing this equation with the general equation of a circle, we have

\[g = – \frac{{{x_1} + {x_2}}}{2},\,\,\,f = – \frac{{{y_1} + {y_2}}}{2},\,\,\,c = {x_1}{x_2} + {y_1}{y_2}\]

Therefore, the centre of the circle is given by

\[\left( { – g, – f} \right) = \left( {\frac{{{x_1} + {x_2}}}{2},\frac{{{y_1} + {y_2}}}{2}} \right)\]

The radius of the circle is given by

\[r = \sqrt {{g^2} + {f^2} – c} = \sqrt {{{\left( { – \frac{{{x_1} + {x_2}}}{2}} \right)}^2} + {{\left( { – \frac{{{y_1} + {y_2}}}{2}} \right)}^2} – \left( {{x_1}{x_2} + {y_1}{y_2}} \right)} \]
\[\begin{gathered} \Rightarrow r = \sqrt {\frac{{{{\left( {{x_1} + {x_2}} \right)}^2} + {{\left( {{y_1} + {y_2}} \right)}^2} – 4\left( {{x_1}{x_2} + {y_1}{y_2}} \right)}}{4}} \\ \Rightarrow r = \frac{{\sqrt {{x_1}^2 + {x_2}^2 + 2{x_1}{x_2} + {y_1}^2 + {y_2}^2 + 2{y_1}{y_2} – 4{x_1}{x_2} – 4{y_1}{y_2}} }}{2} \\ \Rightarrow r = \frac{{\sqrt {{{\left( {{x_1} – {x_2}} \right)}^2} + {{\left( {{y_1} – {y_2}} \right)}^2}} }}{2} \\ \end{gathered} \]

Example:
Find the equation of a circle through the ends $$\left( {5,7} \right)$$ and $$\left( {1,3} \right)$$ of its diameter. Also find the centre and radius.

The equation of the circle through the ends points of its diameter is

\[\left( {x – {x_1}} \right)\left( {x – {x_2}} \right) + \left( {y – {y_1}} \right)\left( {y – {y_2}} \right) = 0\]

Here from the given points we have values $${x_1} = 5,\,\,{x_2} = 1,\,\,{y_1} = 7,\,\,{y_2} = 3$$
Now substitute these values of the given points in the above equation of a circle as

\[\begin{gathered} \left( {x – 5} \right)\left( {x – 1} \right) + \left( {y – 7} \right)\left( {y – 3} \right) = 0 \\ \Rightarrow {x^2} – 6x + 5 + {y^2} – 10y + 21 = 0 \\ \Rightarrow {x^2} + {y^2} – 6x – 10y + 26 = 0 \\ \end{gathered} \]

The centre of the circle is $$\left( {\frac{{{x_1} + {x_2}}}{2},\frac{{{y_1} + {y_2}}}{2}} \right) = \left( {\frac{{5 + 1}}{2},\frac{{7 + 3}}{2}} \right) = \left( {3,5} \right)$$

The radius of the circle is \[r = \frac{{\sqrt {{{\left( {{x_1} – {x_2}} \right)}^2} + {{\left( {{y_1} – {y_2}} \right)}^2}} }}{2} = \frac{{\sqrt {{{\left( {5 – 1} \right)}^2} + {{\left( {7 – 3} \right)}^2}} }}{2} = \frac{{4\sqrt 2 }}{2} = 2\sqrt 2 \]