Equation of the Altitudes of a Triangle
To find the equation of the altitude of a triangle, we examine the following example: Consider the triangle having vertices $$A\left( { – 3,2} \right)$$, $$B\left( {5,4} \right)$$ and $$C\left( {3, – 8} \right)$$.
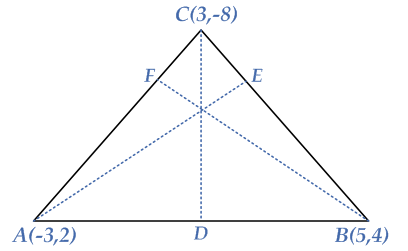
First we find the slope of side $$AB$$:
\[\frac{{4 – 2}}{{5 – \left( { – 3} \right)}} = \frac{2}{{5 + 3}} = \frac{1}{4}\]
The altitude $$CD$$ is perpendicular to side $$AB$$.
The slope of \[CD = – \frac{1}{{{\text{slope}}\,{\text{of}}\,AB}} = – 4\]
Since the altitude $$CD$$ passes through the point $$C\left( {3, – 8} \right)$$, using the point-slope form of the equation of a line, the equation of $$CD$$ is
\[\begin{gathered} y – \left( { – 8} \right) = – 4\left( {x – 3} \right) \\ \Rightarrow y + 8 = – 4x + 12 \\ \Rightarrow 4x + y – 4 = 0 \\ \end{gathered} \]
This is the required equation of the altitude from $$C$$ to $$AB$$.
The slope of side $$BC$$ is
\[\frac{{ – 8 – 4}}{{3 – 5}} = \frac{{ – 12}}{{ – 2}} = 6\]
The altitude $$AE$$ is perpendicular to side $$BC$$.
The slope of \[AE = – \frac{1}{{{\text{slope}}\,{\text{of}}\,BC}} = – \frac{1}{6}\]
Since the altitude $$AE$$ passes through the point $$A\left( { – 3,2} \right)$$, using the point-slope form of the equation of a line, the equation of $$AE$$ is
\[\begin{gathered} y – 2 = – \frac{1}{6}\left( {x – \left( { – 3} \right)} \right) \\ \Rightarrow – 6\left( {y – 2} \right) = x + 3 \\ \Rightarrow x + 6y – 9 = 0 \\ \end{gathered} \]
This is the required equation of the altitude from $$A$$ to $$BC$$.
The slope of side $$AC$$ is
\[\frac{{ – 8 – 2}}{{3 – \left( { – 3} \right)}} = – \frac{{10}}{6} = – \frac{5}{3}\]
The altitude $$BF$$ is perpendicular to side $$AC$$.
The slope of \[BF = – \frac{1}{{{\text{slope}}\,{\text{of}}\,AC}} = \frac{3}{5}\]
Since the altitude $$BF$$ passes through the point $$B\left( {5,4} \right)$$, using the point-slope form of the equation of a line, the equation of $$BF$$ is
\[\begin{gathered} y – 4 = \frac{3}{5}\left( {x – 5} \right) \\ \Rightarrow 5\left( {y – 4} \right) = 3\left( {x – 5} \right) \\ \Rightarrow 3x – 5y + 5 = 0 \\ \end{gathered} \]
This is the required equation of the altitude from $$B$$ to $$AC$$.
