Distance of a Point from a Line
The distance $$d$$ of the point $$A\left( {{x_1},{y_1}} \right)$$ from the line $$ax + by + c = 0$$ is given by
\[d = \frac{{\left| {a{x_1} + b{y_1} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\]
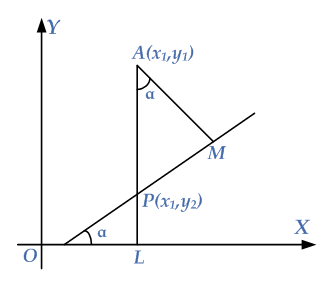
Let $$\alpha $$ be the inclination of the line as shown in the given diagram, and then its slope is given as
\[\tan \alpha = – \frac{a}{b}\]
Squaring both sides of the above value of the slope, we get
\[\begin{gathered} {\tan ^2}\alpha = \frac{{{a^2}}}{{{b^2}}} \\ \Rightarrow {\sec ^2}\alpha – 1 = \frac{{{a^2}}}{{{b^2}}}\,\, \Rightarrow {\sec ^2}\alpha = \frac{{{a^2}}}{{{b^2}}} + 1 \\ \Rightarrow {\sec ^2}\alpha = \frac{{{a^2} + {b^2}}}{{{b^2}}}\,\, \Rightarrow {\cos ^2}\alpha = \frac{{{b^2}}}{{{a^2} + {b^2}}} \\ \Rightarrow \cos \alpha = \pm \frac{b}{{\sqrt {{a^2} + {b^2}} }} \\ \Rightarrow \left| {\cos \alpha } \right| = \frac{{\left| b \right|}}{{\sqrt {{a^2} + {b^2}} }}\,\,\,\,{\text{ – – – }}\left( {\text{i}} \right) \\ \end{gathered} \]
Draw a perpendicular line from point $$A$$ to the X-axis intersecting the line at point $$P$$. Since the abscissa of $$P$$ is the same as that of $$A$$, the coordinates of point $$P$$ are $$\left( {{x_1},{y_2}} \right)$$, $${y_2} \ne {y_1}$$. In the triangle $$ALP$$, $$m\angle MAP = \alpha $$ and $$m\angle AMP = {90^ \circ }$$, so
\[\frac{{AM}}{{AP}} = \cos \alpha \]
\[\begin{gathered} \Rightarrow AM = AP\cos \alpha \\ \Rightarrow d = \left( {AL – PL} \right)\cos \alpha \,\,\,\,\,\,\,\,\,\,\because AM = d,\,\,AM = AL – PL \\ \Rightarrow d = \left( {{y_1} – {y_2}} \right)\cos \alpha \,\,\,\,\,\,\,\,\,\,\,\,\,\because AL = {y_1},\,PL = {y_2} \\ \end{gathered} \]
Since the distance $$d$$ should be positive, we must take the modulus of the right side of the above equation, i.e.
\[d = \left| {{y_1} – {y_2}} \right|\left| {\cos \alpha } \right|\,\,\,\,{\text{ – – – }}\left( {{\text{ii}}} \right)\]
Putting the value of $$\left| {\cos \alpha } \right|$$ from equation (i) in equation (ii), we get
\[d = \left| {{y_1} – {y_2}} \right|\frac{{\left| b \right|}}{{\sqrt {{a^2} + {b^2}} }}\,\,\,\,{\text{ – – – }}\left( {{\text{iii}}} \right)\]
Since the point $$P\left( {{x_1},{y_2}} \right)$$ lies on the line $$ax + by + c = 0$$, then
\[\begin{gathered} a{x_1} + b{y_2} + c = 0 \\ \Rightarrow b{y_2} = – a{x_1} – c \\ \Rightarrow {y_2} = \frac{{ – a{x_1} – c}}{b} \\ \end{gathered} \]
Putting this value in equation (iii), we get
\[d = \left| {{y_1} – \frac{{ – a{x_1} – c}}{b}} \right|\frac{{\left| b \right|}}{{\sqrt {{a^2} + {b^2}} }}\,\,\]
\[\begin{gathered} d = \left| {\frac{{b{y_1} + a{x_1} + c}}{b}} \right|\frac{{\left| b \right|}}{{\sqrt {{a^2} + {b^2}} }} = \frac{{\left| {a{x_1} + b{y_1} + c} \right|}}{{\left| b \right|}}\frac{{\left| b \right|}}{{\sqrt {{a^2} + {b^2}} }} \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow \boxed{d = \frac{{\left| {a{x_1} + b{y_1} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}} \\ \end{gathered} \]
Example: Find the distance of the point $$\left( {2, – 3} \right)$$ from the line $$7x – 5y + 9 = 0$$.
Since the given point is $$\left( {2, – 3} \right)$$, so $${x_1} = 2,\,\,{y_1} = – 3$$
Since the given line is $$7x – 5y + 9 = 0$$, so $$a = 7,\,\,b = – 5,\,\,c = 9$$
The required distance is
\[d = \frac{{\left| {a{x_1} + b{y_1} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }} = \frac{{\left| {7\left( 2 \right) – 5\left( { – 3} \right) + 9} \right|}}{{\sqrt {{7^2} + {{\left( { – 3} \right)}^2}} }} = \frac{{38}}{{\sqrt {74} }}\]
