The Area of a Rectangle
A rectangle is a quadrilateral in which all four angles are right angles and the opposite sides are equal in length.
Let $$ABCD$$ be a rectangle having $$AB = a$$ and $$BC = b$$. Let $$AC$$ be the diagonal which divides the rectangle into two right triangles, $$\Delta ABC$$ and $$\Delta ADC$$.
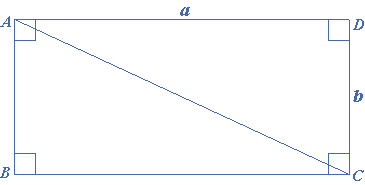
\[\begin{gathered} {\text{Area of }}\Delta ABC = \frac{1}{2}AB \times BC = \frac{1}{2}a \times b \\ \Rightarrow {\text{Area of }}\Delta ADC = \frac{1}{2}DC \times AD = \frac{1}{2}a \times b \\ \end{gathered} \]
\[\begin{gathered} {\text{Area of rectangle }}ABCD = {\text{Area of }}\Delta ABC + {\text{Area of }}\Delta ADC \\ \Rightarrow {\text{Area of rectangle }}ABCD = \frac{1}{2}a \times b + \frac{1}{2}a \times b \\ \therefore {\text{Area of rectangle }}ABCD = a \times b = {\text{length}} \times {\text{breadth}} \\ \end{gathered} \]
Example:
In exchange for a square plot of land, one of whose sides is $$84$$ m, a man wants to buy a rectangular plot $$144$$m long which is of the same area as the square plot. Find the width of the rectangular plot.
Solution:
One side of the square plot $$ = 84$$ m.
The area of the square plot $$ = 84 \times 84 = 7056$$ square m.
The length of the rectangular plot $$ = 144$$ m.
The length of the rectangular plot $$ = $$ area of the square plot.
The length of the rectangular plot $$ = 7056$$ square m.
$$\therefore $$ the width of the rectangular plot $$ = \frac{{7056}}{{144}} = 49$$ m
Example:
How many tiles $$20$$cm square will be required to pave a footpath $$1$$m wide going around the outside of a grassy plot $$28$$ m long and $$18$$ m wide.
Solution:
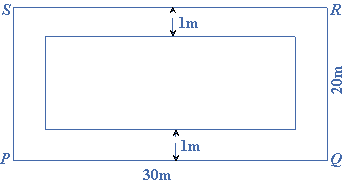
The width of the foot path $$ = 1$$ m.
The outside dimensions of the plot are $$28 + 2 = 30$$ m and $$18 + 2 = 20$$ m.
Now,
The outside area of the plot $$PQRS = 30 \times 20 = 600$$ square m.
The inside area of the plot $$ABCD = 28 \times 18 = 504$$ square m.
The area of the foot path $$ = $$ outside area $$ – $$inside area $$ = 600 – 504 = 96$$ square m.
The area of one tile $$ = \frac{{20}}{{100}} \times \frac{2}{{100}} = 0.04$$ square m.
The number of tiles required $$ = \frac{{96}}{{0.04}} = 2400$$ tiles.
