Angle of Intersection of Two Lines
Let $${l_1}$$ and $${l_2}$$ be two coplanar and non-parallel lines with inclination $${\alpha _1}$$ and $${\alpha _2}$$ respectively, as shown in the given diagram. The angle of intersection of lines $${l_1}$$ and $${l_2}$$ is the angle $$\theta $$ through which line $${l_1}$$ is rotated counter-clockwise about the point of intersection so that it coincides with $${l_2}$$.
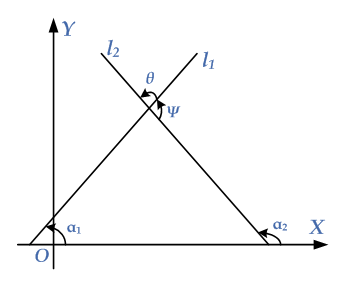
The angle $$\theta $$ is the angle of the intersection of lines $${l_1}$$ and $${l_2}$$ measured from $${l_2}$$ to $${l_1}$$. The angle $$\psi $$ is also the angle of intersection of lines $${l_1}$$ and $${l_2}$$ measured from $${l_2}$$ to $${l_1}$$. If the lines are not perpendicular, then one angle between them is an acute angle.
Theorem: The angle $$\theta $$ of the intersection of two non-vertical lines $${l_1}$$ and $${l_2}$$ from $${l_2}$$ to $${l_1}$$ is given by $$\tan \theta = \frac{{{m_2} – {m_1}}}{{1 + {m_1}{m_2}}}$$, where $${m_1}$$ and $${m_2}$$ are the slopes of lines $${l_1}$$ and $${l_2}$$ respectively.

Proof: Let $${l_1}$$ and $${l_2}$$ be two coplanar and non-parallel lines with inclination $${\alpha _1}$$ and $${\alpha _2}$$ respectively, as shown in the given diagram. It is clear from the diagram that
\[\begin{gathered} {\alpha _1} + \theta = {\alpha _2} \\ \Rightarrow \theta = {\alpha _2} – {\alpha _1} \\ \Rightarrow \tan \theta = \tan \left( {{\alpha _2} – {\alpha _1}} \right) \\ \Rightarrow \tan \theta = \frac{{\tan {\alpha _2} – \tan {\alpha _1}}}{{1 + \tan {\alpha _1}\tan {\alpha _2}}}\,\,\,\,{\text{ – – – }}\left( {\text{i}} \right) \\ \end{gathered} \]
Since $${\alpha _1}$$ and $${\alpha _2}$$ are the inclination of lines $${l_1}$$ and $${l_2}$$ respectively, their slopes are $${m_1} = \tan {\alpha _1}$$, $${m_2} = \tan {\alpha _2}$$. Putting these values of $$\tan {\alpha _1}$$, $$\tan {\alpha _2}$$ in equation (i), we have
\[ \Rightarrow \boxed{\tan \theta = \frac{{{m_2} – {m_1}}}{{1 + {m_1}{m_2}}}}\]
If the lines $${l_1}$$ and $${l_2}$$ are perpendicular, then $$\theta = {90^ \circ }$$, and using above formula, we have
\[\begin{gathered} 1 + {m_1}{m_2} = \frac{{{m_2} – {m_1}}}{{\tan \theta }} \\ \Rightarrow 1 + {m_1}{m_2} = \frac{{{m_2} – {m_1}}}{{\tan {{90}^ \circ }}} \\ \Rightarrow 1 + {m_1}{m_2} = \frac{{{m_2} – {m_1}}}{\infty }\,\,\, \Rightarrow 1 + {m_1}{m_2} = 0 \\ \end{gathered} \]
\[\boxed{{m_1}{m_2} = – 1}\]
This is the condition for two lines to be perpendicular.
