The Area Bounded by the Curve y=x^3-x and the x-axis

In this tutorial we shall find the area bounded by the curve y = {x^3} - x and the x-axis.

Since y = 0 at the x-axis, for the points of intersection of the curve y = {x^3} - x at x-axis, put y = 0. This implies that {x^3} - x = 0

\begin{gathered} \Rightarrow x\left( {{x^2} - 1} \right) = 0 \\ \Rightarrow x\left( {x - 1} \right)\left( {x + 1} \right) = 0 \\ \Rightarrow x = - 1,\,\,\,x = 0,\,\,\,x = 1 \\ \end{gathered}

The curve cuts the x-axis only at x = - 1,\,\,\,x = 0,\,\,\,x = 1, as shown by the graph of the given function y = {x^3} - x.


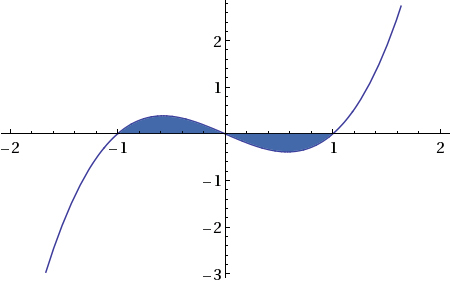
area-bounded-curve-x-axis

It is also clear from the graph above that y \geqslant 0 for - 1 \leqslant x \leqslant 0 and y \leqslant 0 for 0 \leqslant x \leqslant 1, so the required area is split into two regions and is given by

A = \int\limits_{ - 1}^0 {ydx} + \int\limits_0^1 { - ydx}


\begin{gathered} A = \int\limits_{ - 1}^0 {\left( {{x^3} - x} \right)dx} - \int\limits_0^1 {\left( {{x^3} - x} \right)dx} \\ \Rightarrow A = \left| {\frac{{{x^4}}}{4} - \frac{{{x^2}}}{2}} \right|_{ - 1}^0 - \left| {\frac{{{x^4}}}{4} - \frac{{{x^2}}}{2}} \right|_0^1 = 0 - \left( {\frac{1}{4} - \frac{1}{2}} \right) - \left( {\frac{1}{4} - \frac{1}{2}} \right) + 0 \\ \Rightarrow A = - \frac{1}{4} + \frac{1}{2} - \frac{1}{4} + \frac{1}{2} = \frac{1}{2} \\ \end{gathered}


Area = \frac{1}{2}