Nature of Functions
One – One Function:
Let ‘A’ and ‘B’ be any two non–empty sets, then a function ‘$$f$$’ from A to B is called a one–one function, if and only if distinct elements of set A have distinct elements of set B.
e.g. $${\text{A}}\left\{ {1,2,3} \right\}$$, $${\text{B}}\left\{ {{\text{a}},{\text{b}},{\text{c}}} \right\}$$

Mathematically,
Let $$f:{\text{A}} \to {\text{B}}$$ be a function then ‘$$f$$’ is called a one–one function if and only if
(i) $$f\left( {{{\text{x}}_1}} \right) \ne f\left( {{{\text{x}}_2}} \right) \Rightarrow {{\text{x}}_1} \ne {{\text{x}}_2}\;,\;\;\;\forall \;{{\text{x}}_1},{{\text{x}}_2} \in {\text{A}}$$
(ii) $$f\left( {{{\text{x}}_1}} \right) = f\left( {{{\text{x}}_2}} \right) \Rightarrow {{\text{x}}_1} = {{\text{x}}_2}\;,\;\;\;\forall \;{{\text{x}}_1},{{\text{x}}_2} \in {\text{A}}$$
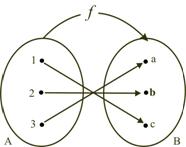
Onto Function:
Let ‘A’ and ‘B’ be any two non–empty sets, then a function ‘$$f$$’ from A to B is called an onto function if and only if the range of $$f = {\text{B}}$$
e.g. $${\text{A}}\left\{ {1,2,3} \right\}$$, $${\text{B}}\left\{ {{\text{a}},{\text{b}}} \right\}$$
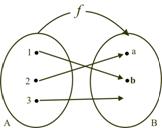
Bijective Function:
A function which is one–one as well as an onto function is called a bijective function.
e.g.$${\text{A}} = \left\{ {1,2,3} \right\}$$, $${\text{B}} = \left\{ {{\text{a}},{\text{b}},{\text{c}}} \right\}$$