Skewness:
            Lack of symmetry is called Skewness. If a distribution is not symmetrical then it is called skewed distribution. So, mean, median and mode are different in values and one tail becomes longer than other. The skewness may be positive or negative.

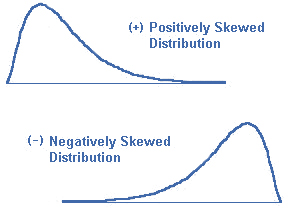
Positively skewed distribution:
            If the frequency curve has longer tail to right the distribution is known as positively skewed distribution and Mean > Median > Mode.

Positively skewed distribution:
            If the frequency curve has longer tail to left the distribution is known as negatively skewed distribution and Mean < Median < Mode.

Measure of Skewness:
            The difference between the mean and mode gives as absolute measure of skewness. If we divide this difference by standard deviation we obtain a relative measure of skewness known as coefficient and denoted by SK.
            Karl Pearson coefficient of Skewness
                                    
            Sometimes the mode is difficult to find. So we use another formula
                                    
            Bowley’s  coefficient of Skewness