A random variable is called continuous if it can assume all possible values in the possible range of the random variable. Suppose the temperature in a certain city in the month of June in the past many years has always been between  to  centigrade. The temperature can take any value between the ranges  to. The temperature on any day may be  or  or it may take any value between  and. When we say that the temperature is, it means that the temperature lies between somewhere between  to. Any observation which is taken falls in the interval. There is nothing like an exact observation in the continuous variable. In discrete random variable the values of the variable are exact like 0, 1, 2 good bulbs. In continuous random variable the value of the variable is never an exact point. It is always in the form of an interval, the interval may be very small.

            Some examples of the continuous random variables are:

1. The computer time (in seconds) required to process a certain program.
2. The time that a poultry bird will gain the weight of 1.5 kg.
3. The amount of rain falls in the certain city.
4. The amount of water passing through a pipe connected with a high level reservoir.
5. The heat gained by a ceiling fan when it has worked for one hour.

Probability Density Function:
            The probability function of the continuous random variable is called probability density function of briefly p.d.f. It is denoted by  where  is the probability that the random variable  takes the value between  and  where is a very small change in .

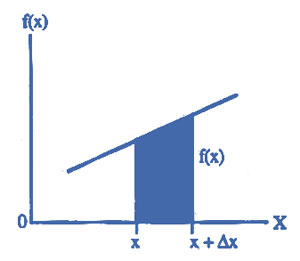
If there are two points ‘a’ and ‘b’ then the probability that the random variable will take the value between a and b a given by the management.

            Where ‘a’ and ‘b’ are the points between  and . The quantity  is called probability differential.
The number of possible outcomes of a continuous random variable is uncountable infinite. Therefore, a probability of zero is assigned to each point of the random variable. Thus  for all values of. This means that we must calculate a probability for a continuous random variable over an internal and not for any particular point. This probability can be interpreted as an area under the graph between the interval from a to b. When we say that the probability is zero that a continuous random variable assumes a specific value, we do not necessarily mean that a particular value cannot occur. We in fact, mean that the point (event) is one of an infinite number of possible outcomes. Whenever we have to find the probability of some interval of the continuous random variable, we can use any one of these two methods.

1. Integral calculus.
2. Area by geometrical diagrams (this method is easy to apply when  is a simple linear function).

Properties of Probability Density Function:
            The probability density function  must have the following properties.

1. It is non-negative i.e.  for all
2. 
3.      Where c is any constant
4. As probability of area for  (constant), therefore . If we take an interval a to b. It makes no difference whether end points of the interval are considered or not. Thus we can write:
   
5. 

Example:
            A continuous random variable X which can assume between  and 8 inclusive, has a density function given by  where  is a constant.
            (a)  Calculate             (b)      (c) 

Solution:
           

           (a)   will be density functions if (i)  for every x and (ii) . If ,  is clearly for every x in the given interval. Hence for  to be density function, we have

           
           
So that
Therefore,

          (b)  

           (c)