X and Y Intercepts of a Line
When a straight line is represented graphically the following two main attributes will come out: the $$X$$-intercept and the $$Y$$-intercept of the straight line. These two concepts are very simple and easy to understand when we draw a straight line graphically.
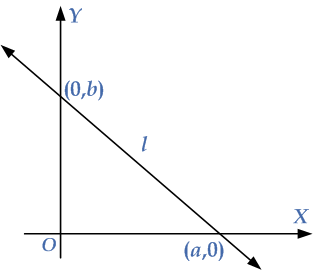
The $$X$$-intercept occurs when we draw a straight in a Cartesian plane, i.e. $$XY$$-plane, and the straight line cuts the $$X$$-axis at one point, say $$a$$. This point of intersection is called the $$X$$-intercept of a straight line and at the point value of the $$Y$$-axis is zero, i.e. $$y = 0$$. The $$X$$-intercept is usually represented by an ordered pair: $$\left( {a,0} \right)$$.
Similarly, the $$Y$$-intercept occurs when the straight line cuts the $$Y$$-axis at one point, say $$b$$. This point of intersection is called the $$Y$$-intercept of a straight line and at this point value of the X-axis is zero, i.e. $$x = 0$$. The $$Y$$-intercept is usually represented by an ordered pair: $$\left( {0,b} \right)$$.
Algebraically we can find the $$X$$-intercept and $$Y$$-intercept of a straight line $$ax + by + c = 0$$ by setting the values $$y = 0$$ and $$x = 0$$ respectively.
Example: Find the $$X$$- and $$Y$$-intercepts of the given straight line: $$2x + 4y = 16$$
To find the $$X$$-intercept put $$y = 0$$ in the above equation of a straight line:
\[2x + 4\left( 0 \right) = 16 \Rightarrow x = 8\]
Therefore, the $$X$$-intercept is $$\left( {8,0} \right)$$.
Similarly, to find the $$Y$$-intercept put $$x = 0$$ in the above equation of a straight line:
\[2\left( 0 \right) + 4y = 16 \Rightarrow y = 4\]
Therefore, the $$Y$$-intercept is $$\left( {0,4} \right)$$.
