Prism Types

Cube

The cube is a right prism with a square base and a height which is same as the side of the base. Let $$a$$ be the side of the cube, then

1. The volume of the cube $$ = $$ area of base $$ \times $$ height       i.e. $$V = {a^3}$$
2. The total surface area of the cube $$ = $$ area of six faces       i.e. $$S = 6{a^2}$$
3. The line joining the opposite corners of the cube is called the diagonal of the cube. The length of the diagonal of the cube $$ = a\sqrt 3 $$

Proof: In the given figure, the line $$DF$$ is the diagonal of the cube.

$$\angle DBF = {90^ \circ }$$
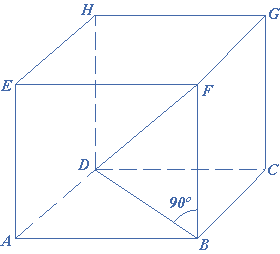
$$\therefore $$            $$D{F^2} = B{D^2} + B{F^2}$$
But      $$B{D^2} = A{B^2} + A{D^2}$$
$$\therefore $$            $$D{F^2} = A{B^2} + A{D^2} + B{F^2}$$

Since $$AB,AD$$ and $$BF$$ are the sides of the cube and each has a length equal to $$a$$, therefore
$$D{F^2} = {a^2} + {a^2} + {a^2} = 3{a^2}$$
$$\therefore $$            $$DF = a\sqrt 3 $$

Example:

Three cubes of metal whose edges are in the ratio $$3:4:5$$ are melted into a single cube whose diagonal is $$12\sqrt 3 $$ cm. Find the edges of the three cubes.

Solution:

Let the edges of the cubes be $$3x,4x$$ and $$5x$$ cm
$$\therefore $$ their volumes are:
$${\left( {3x} \right)^2},{\left( {4x} \right)^2}$$and $${\left( {5x} \right)^2}$$cu. cm
$$27{x^3},64{x^3}$$ and $$125{x^3}$$cu. cm
$$\therefore $$ the volume of the single cube $$ = 27{x^3} + 64{x^3} + 125{x^3} = 216{x^3}$$ cu. cm

Let $$a$$ be the edges of the cube, then volume:
$$\therefore $$ $${a^3} = 216{x^3} = {\left( {6x} \right)^3}$$       $$ \Rightarrow a = 6$$
$$\therefore $$ edge $$a = 6x$$ cm

Now, the diagonal of the cube $$ = \sqrt 3 \times {\text{edge}}$$
$$ = \sqrt 3 \times 6x$$ cm

But, the diagonal of the cube $$ = 12\sqrt 3 $$
$$\therefore $$ $$\sqrt 3 \times 6x = 12\sqrt 3 $$       $$ \Rightarrow x = 2$$

Hence the three edges of the cube are $$6{\text{ cm, }}8{\text{ cm}}$$ and $$10{\text{ cm}}$$

Rectangular Prism

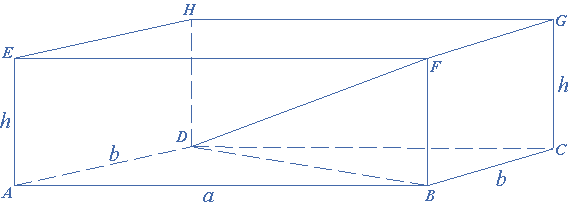
(1) The volume of the rectangular prism $$ = $$ area of base $$ \times $$ height
$$V = a \cdot b \cdot h$$

(2) The total surface area $$ = $$ area of six faces
The total surface area $$ = 2ab + 2bh + 2ah \Rightarrow S = 2\left( {ab + bh + ah} \right)$$

(3) The length of the diagonal is
$$D{F^2} = B{D^2} + F{B^2}$$
$$ = {a^2} + {b^2} + {h^2}$$       (as$$AD = BC = b$$, $$FB = CG = h$$)
$$DF = \sqrt {{a^2} + {b^2} + {h^2}} $$

 

Example:

The length, width and thickness of a rectangular block are $$9.6,13.2$$ and $$14.3$$ cm respectively. Find the volume, surface area and length of the diagonal of the block.

Solution:

Given that: $$a = 9.6$$ cm, $$b = 13.2$$ cm, $$h = 14.3$$ cm

(1) Volume $$V = a \cdot b \cdot h = 9.6 \times 13.2 \times 14.3 = 1812$$ cu. cm

(2) Surface area $$S = 2\left( {ab + bh + ah} \right) = 2\left( {12.6 + 13.2 + 14.3} \right) = 905.52$$ sq.cm

(3) Length of diagonal $$ = \sqrt {{a^2} + {b^2} + {h^2}} = \sqrt {{{\left( {9.6} \right)}^2} + {{\left( {13.2} \right)}^2} + {{\left( {14.3} \right)}^2}} = 21.7\,cm$$

Polygonal Prism

A prism with a polygon base is known as a polygonal prism.

(a) The volume of a prism whose base is a rectangular polygon of $$n$$ sides and height $$h = $$ area of the base $$ \times $$ height.

1. $$V = \left( {\frac{{n{a^2}}}{4}\cot \frac{{{{180}^ \circ }}}{n}} \right) \times h$$   when side $$a$$ is given.
2. $$V = \left( {n{r^2}\tan \frac{{{{180}^ \circ }}}{n}} \right) \times h$$ when the radius $$r$$ of the inscribed circle is given.
3. $$V = \left( {\frac{{n{R^2}}}{4}\sin \frac{{{{180}^ \circ }}}{n}} \right) \times h$$   when the radius $$R$$ of the circumscribed circle is given.

(b) The lateral surface area $$ = $$ perimeter of base $$ \times $$ height

1. $$L.S = na \times h$$   when side $$a$$ is given.
2. $$L.S = 2nr\tan \frac{{{{180}^ \circ }}}{n} \times h$$   when the radius $$r$$of the inscribed circle is given.
3. $$L.S = 2nR\sin \frac{{{{180}^ \circ }}}{n} \times h$$   when the radius $$R$$ of the circumscribed circle is given.

(c) The total surface area $$ = $$ lateral surface area $$ + $$ area of base and top

 

Example:

A pentagonal prism which has its base circumscribed about a circle of radius $$1$$ dm, and which has a height of $$8$$ dm is formed into a cube. Find the size of the cube.

Solution:

Here $$n = 5$$ dm, $$r = 1$$ dm, $$h = 8$$ dm

Since the volume of the material remains the same in both cases
$$\therefore $$ the volume of the cube $$ = $$ the volume of the pentagonal prism.

Now, the volume of the pentagonal prism is
\[\begin{gathered} {\text{area}} \times {\text{height}} = \left( {n{r^2}\tan \frac{{{{180}^ \circ }}}{n}} \right) \times h = \left( {5{{\left( 1 \right)}^2}\tan \frac{{{{180}^ \circ }}}{5}} \right) \times 8 = 40\tan {36^ \circ } \\ {\text{area}} \times {\text{height}} = 40 \times 0.7265 = 29.06 = {a^3} \\ \end{gathered} \]

Now by the condition
$${a^3} = 29.06 \Rightarrow a = {\left( {29.06} \right)^{\frac{1}{3}}}$$

Taking $$\log $$ both sides, we get
$$\log a = \frac{1}{3}\log 29.06 = \frac{1}{3}\left( {1.2633} \right) = 0.4877$$

Taking $$anti\log $$, we get $$a = 3.07$$dm.