The Two Points Form of the Equation of a Line
The equation of a non-vertical line passing through two points $$A\left( {{x_1},{y_1}} \right)$$ and $$B\left( {{x_2},{y_2}} \right)$$ is given by
\[\frac{{x – {x_1}}}{{{x_2} – {x_1}}} = \frac{{y – {y_1}}}{{{y_2} – {y_1}}}\]
To prove this equation let $$P\left( {x,y} \right)$$ be any point on the given line $$l$$. Also this line passes through $$A\left( {{x_1},{y_1}} \right)$$ and $$B\left( {{x_2},{y_2}} \right)$$, as shown in the given diagram.
From $$A$$ and $$B$$ draw $$AL$$ and $$BN$$ perpendicular to the X-axis and from point $$P$$ draw $$PM$$ also perpendicular to the X-axis. Also from $$A$$ draw perpendicular to $$AD$$ on $$BN$$.
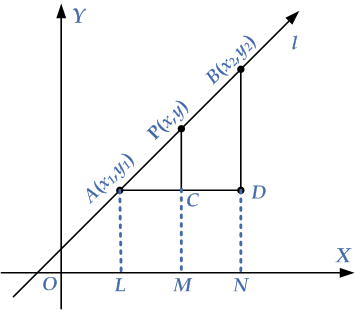
Now from the given diagram, consider the similar triangles $$ADB$$ and $$ACP$$, and by the definition of a slope we take
\[\frac{{PC}}{{BD}} = \frac{{AC}}{{AD}}\,\,\,{\text{ – – – }}\left( {\text{i}} \right)\]
Also from the given diagram we have
\[\begin{gathered} PC = PM – CM = y – {y_1} \\ \Rightarrow BD = BN – DN = {y_2} – {y_1} \\ \Rightarrow AC = LM = OM – ON = x – {x_1} \\ \Rightarrow AD = LN = ON – OL = {x_2} – {x_1} \\ \end{gathered} \]
Putting these all values in the above equation (i) we have
\[\frac{{x – {x_1}}}{{{x_2} – {x_1}}} = \frac{{y – {y_1}}}{{{y_2} – {y_1}}}\]
This is the equation of a line passing through two points $$A\left( {{x_1},{y_1}} \right)$$ and $$B\left( {{x_2},{y_2}} \right)$$. This equation can also have the form \[\frac{{x – {x_2}}}{{{x_1} – {x_2}}} = \frac{{y – {y_2}}}{{{y_1} – {y_2}}}\]
In determinant form, the given equation of a line through two points is
\[\left| {\begin{array}{*{20}{c}} x&y&1 \\ {{x_1}}&{{y_1}}&1 \\ {{x_2}}&{{y_2}}&1 \end{array}} \right| = 0\]
NOTE: There is an alternate way to prove the two points form of the equation of a straight line.
Consider the slope point form of the equation of a line, we have
\[y – {y_1} = m\left( {x – {x_1}} \right)\,\,\,{\text{ – – – }}\left( {\text{i}} \right)\]
Since the line is passing through the point $$\left( {{x_1},{y_1}} \right)$$ in the above equation and the slope of the line is $$m = \frac{{{y_2} – {y_1}}}{{{x_2} – {x_1}}}$$, so equation (i) becomes
\[\begin{gathered} y – {y_1} = \left( {\frac{{{y_2} – {y_1}}}{{{x_2} – {x_1}}}} \right)\left( {x – {x_1}} \right) \\ \frac{{x – {x_2}}}{{{x_1} – {x_2}}} = \frac{{y – {y_2}}}{{{y_1} – {y_2}}} \\ \end{gathered} \]
