Introduction to Parabola

In this tutorial we shall study the parabola, which is obtained by the intersection of the plane and a right circular cone when the plane is parallel to an element of the cone. The conic is a parabola if the eccentricity is equal to 1. The following is the analytic definition of the parabola.

Definition of the Parabola:
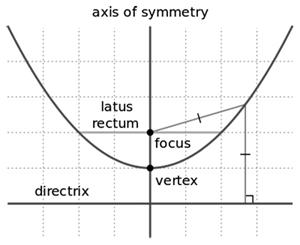
The parabola is defined as the locus of a point $$P\left( {x,y} \right)$$ which moves so that it is always equidistant to a given line and a given point. The line through the focus which is perpendicular to the directrix is called the axis of the parabola. The point midway between the directrix and the focus is the vertex of the parabola. The line through the focus perpendicular to the axis and intercepted by the parabola is called the latus rectum of a focal chord and the length of the focal chord is called the focal width.

There are so many applications of the parabola in everyday life. For example, if you throw a ball it will attain a parabolic path, or when fighter jets fire a missile it also moves in a parabolic path. One of the important applications of the parabola is the parabolic dish antenna.