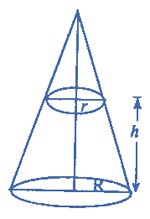
Frustum of a Cone
If a cone is cut by a plane parallel to its base, the portion of a solid between this plane and the base is known as the frustum of a cone.
The volume denoted by $$ABCD$$ in the figure is the frustum of the cone $$ABE$$.

Volume of the Frustum of a Cone
Since we know that cone is a limit of a pyramid, therefore the frustum of a cone will be the limit of the frustum of a pyramid. But the volume of a pyramid is
\[V = \frac{1}{3}h\left[ {{A_1} + {A_2} + \sqrt {{A_1}{A_2}} } \right]\]
Where $${A_1} = \pi {R^2}$$
$${A_2} = \pi {r^2}$$
$$\therefore $$ $$ = \frac{h}{3}\left( {\pi {R^2} + \pi {r^2} + \pi \sqrt {{R^2}{r^2}} } \right)$$
$$ = \frac{{\pi h}}{3}\left( {{R^2} + {r^2} + Rr} \right)$$
A cone 12cm high is cut 8cm from the vertex to form a frustum with a volume of 190cu.cm. Find the radius of the cone.
Solution:
Given that
Height of cone $$ = 12{\text{cm}}$$
Height of the frustum $$h = 12 – 8 = 4{\text{cm}}$$
Volume of the frustum $$ = 190{\text{cu}}.{\text{cm}}$$
Now the volume of the frustum cone
$$ = \frac{{\pi h}}{3}\left( {{R^2} + {r^2} + Rr} \right)$$
or $$190 = \frac{{3.1415 \times 4}}{3}\left[ {\left( {\frac{2}{3}{r^2}} \right) + {r^2} + \frac{2}{3}{r^2}} \right] = 4.19 \times \frac{{19}}{9}{r^2}$$
or $${r^2} = \frac{{190 \times 9}}{{19 \times 4.19}} = \frac{{1710}}{{79.61}} = 21.48$$
$$r = \sqrt {21.40} = 4.63$$
Hence the required radius of the cone $$ = 4.63$$
Curved Surface Area of the Frustum of a Cone
Since a cone is the limiting case of a pyramid, therefore the lateral surface of the frustum of a cone can be deduced from the slant surface of the frustum of a pyramid, i.e. the curved (lateral) surface of the frustum of the cone.
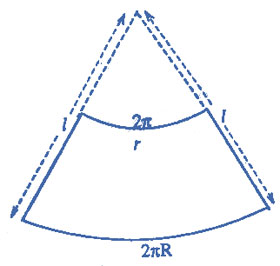
$$ = \frac{1}{2}\left( {{\text{sum of circumferences of bases}}} \right) \times \left( {{\text{slant height}}} \right)$$
$$ = \frac{1}{2}\left( {2\pi R + 2\pi r} \right)l\,\,\, = \pi \left( {R + r} \right)l$$
$$l$$, being the slant height of the frustum, $$R$$ and $$r$$ being the two radii of bases.
Note:
(1) Total surface area of the frustum of a cone
\[ = \pi {R^2} + \pi {r^2} + \pi \left( {R + r} \right)l\]
(2) To find the slant height of the cone, use the Pythagorean theorem.
Example:
A bucket is in the shape of the frustum of a right circular cone, as shown in the figure below. Find the volume and the total surface area of the bucket.
Solution:

Slant height $$l = \sqrt {{h^2} + {r^2}} \,\,\, = \sqrt {{{\left( {17} \right)}^2} + {{\left( {2.5} \right)}^2}} \,\,\, = 17{\text{cm}}$$
Lateral surface area $$ = \pi \left( {R + r} \right)l$$
$$ = \pi \left( {7.5 + 5} \right)\left( {17} \right)\,\,\,\, = 670\,{\text{sq}}{\text{.cm}}$$
$$\therefore $$ Base areas $$ = \pi {R^2} + \pi {r^2}\,\,\,\, = \pi \left( {{R^2} + {r^2}} \right)$$
$$ = \pi \left( {56.25 + 25} \right)\,\,\,\, = 177 + 79$$
$$\therefore $$ Total surface area $$ = \pi {R^2} + \pi {r^2} + \pi \left( {R + r} \right)l$$
$$ = 177 + 79 + 670$$
$$ = 926\,{\text{sq}}{\text{.cm}}$$
Volume $$ = \frac{{\pi h}}{3}\left( {{R^2} + {r^2} + Rr} \right)$$
$$ = \frac{{17h}}{3}\left( {{{\left( {7.5} \right)}^2} + {{\left( 5 \right)}^2} + \left( {7.5} \right)\left( 5 \right)} \right)$$
$$ = 2114\,{\text{cu}}{\text{.cm}}$$

ASA
November 24 @ 7:11 pm
l (slant height) is wrongly mentioned in the diagram of curved surface area.