Equation of a Line Parallel to Another Line
Consider we have the given equation of a line, and this line is parallel to another line which passes through any given point and we must find the required equation of the line with the help of the given line.
Now we explain this concept with the help of an example.
Example: Find the equation of a straight line passing through the point $$\left( {1,2} \right)$$ and is parallel to another given line whose equation is $$2x – 3y + 5 = 0$$.
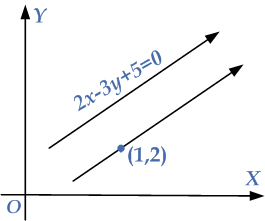
First find the slope of the given line by comparing the slope intercept form of a line as follows:
\[\begin{gathered} 2x – 3y + 5 = 0 \\ \Rightarrow 3y = 2x + 5 \\ \Rightarrow y = \frac{2}{3}x + \frac{5}{3} \\ \end{gathered} \]
Compare this with the slope intercept form to find the slope of line $$y = mx + c$$.
Now the slope of the given line is $$m = \frac{2}{3}$$, since the given line is parallel to the required line and we know that the slope of the parallel is the same, i.e. under the condition of parallel lines $${m_1} = {m_2}$$
Now the slope of the required line is also equals to $$m = \frac{2}{3}$$, since the required line passes through the given point $$\left( {1,2} \right)$$. We find the equation of the required line using the slope point form, which is given by:
\[\begin{gathered} y – {y_1} = m\left( {x – {x_1}} \right) \\ \Rightarrow y – 2 = \frac{2}{3}\left( {x – 1} \right) \\ \Rightarrow 3y – 6 = 2x – 2 \\ \Rightarrow 2x – 3y + 4 = 0 \\ \end{gathered} \]
This is the equation of a straight line parallel to the line $$2x – 3y + 5 = 0$$. In this calculated equation, observe that the coefficients of $$x$$ and $$y$$ are the same.
