Equation of a Line with X-Intercept

Consider the straight line $l$ and let $\alpha$ be the inclination of the straight line as shown in the given diagram. Now the slope of the line is represented by $\tan \alpha = m$ . Let $P\left( {x,y} \right)$ be any point on the given line $l$ . Let $a$ be the X-intercept of the straight line, so the line must pass through the point $A\left( {a,0} \right)$ .

Take $a$ as the X-intercept of the straight line so the line must pass through the point $A\left( {a,0} \right)$ , i.e. $OA = a =$ X-intercept. From point $P$ draw $PQ$ perpendicular to the $X$ -axis.

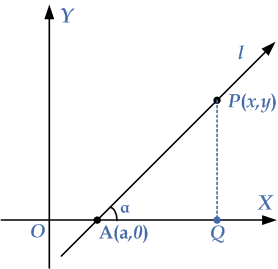
Now from the given diagram, consider the triangle $\Delta PAQ$ , i.e. $m\angle PAQ = \alpha$ , and by the definition of slope we take

$\begin{gathered} \tan \alpha = \frac{{PQ}}{{AQ}} = \frac{{PQ}}{{OQ - OA}} \\ \Rightarrow \,\tan \alpha = \frac{y}{{x - a}} \\ \end{gathered}$

Now by the definition we can use $m$ instead of $\tan \alpha$ , and we get

$\begin{gathered} \Rightarrow m = \frac{y}{{x - a}} \\ \Rightarrow m\left( {x - a} \right) = y \\ \end{gathered}$

$\boxed{y = m\left( {x - a} \right)}$

This is the equation of a straight line having the slope $m$ and X-intercept $a$ .

NOTE: It may be noted that if the line passes through the origin $\left( {0,0} \right)$ , then the X-intercept is equal to zero, i.e. $a = 0$ , so the equation of the straight line becomes $y = mx$ .