The Area of a Trapezoid
A trapezoid is a quadrilateral with two sides parallel and the other two unparallel. The parallel sides of a trapezoid are called the bases. The altitude is the perpendicular distance between the bases.
Let $$ABCD$$ be a trapezoid whose sides $$AB$$ and $$CD$$ are parallel, and $$CB$$ and $$AD$$ are the unparallel sides. Let $$a$$ and $$b$$ be the lengths of the parallel sides and $$h$$ be the height of the trapezoid.
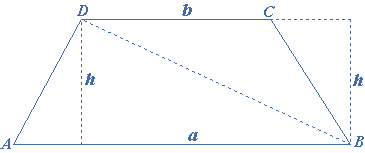
The diagonal of a trapezoid divides it into two triangles that have the same altitude and have as their bases the bases of the trapezoid. Therefore, in the trapezoid $$ABCD$$, the diagonal $$BD$$ divides it into triangles $$ABD$$ and $$BCD$$.
The area of the trapezoid $$ = {\text{Area of }}\Delta ABD + {\text{Area of }}\Delta BDC$$
The area of the trapezoid $$ = \frac{1}{2}AB \times h + \frac{1}{2}DC \times h = \frac{1}{2}(AB + DC) \times h = \frac{1}{2}(a + b) \times h$$
The area of the trapezoid $$ = \frac{{{\text{Sum of parallel sides}}}}{2} \times {\text{height}}$$
Example:
The section of an open channel is a trapezoid, the vertical height of which is $$3$$ m and the breadth of the bottom is $$2$$ m. The inclination of the sides to the horizontal is $$60^\circ $$ outwards. Find the area.
Solution:
Given that $$AD = NM = 2$$ m and $$AM = 3$$ m
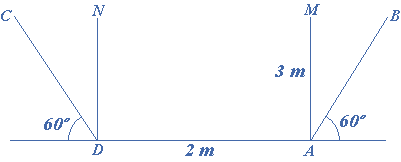
The area of the trapezoid $$ = \frac{{{\text{Sum of parallel sides}}}}{2} \times h = \frac{{AD + BC}}{2} \times AM$$
But the parallel sides are $$AD$$ and $$CB$$
$$BC = BM + MN + NC$$…(i)
Now $$\frac{{BM}}{{AM}} = \cot 60^\circ $$
$$MB = AM\cot 60^\circ = 3 \times \frac{1}{{\sqrt 3 }} = 1.732$$
Similarly, $$NC = 1.732$$ and (i) gives
$$BC = 1.732 + 2 + 1.732 = 5.464$$
The area of the trapezoid $$ = \frac{{{\text{2}} \times {\text{5}}{\text{.464}}}}{2} \times 3 = \frac{{7.464}}{2} \times 3 = 3.732 \times 3 = 11.196$$ square m.
