The Area of a Square
A square is a quadrilateral whose four angles are all right angles and whose all sides are equal.
Let $$ABCD$$ be a square with each side in length equal to $$a$$ and $$AC$$ is a diagonal which divides the square $$ABCD$$ into two equal triangles, $$\Delta ABC$$ and$$\Delta ACD$$. Since $$ABC$$ is a right triangle, therefore:
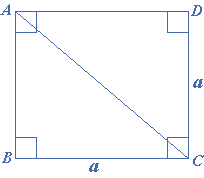
\[\begin{gathered} {\text{Area of }}\Delta ABC = \frac{1}{2}AB \times BC \\ \Rightarrow {\text{Area of }}\Delta ABC = \frac{1}{2}a \times a = \frac{1}{2}{a^2} \\ \end{gathered} \]
Similarly,
\[\begin{gathered} {\text{Area of }}\Delta ACD = \frac{1}{2}CD \times AD \\ \Rightarrow {\text{Area of }}\Delta ACD = \frac{1}{2}a \times a = \frac{1}{2}{a^2} \\ \end{gathered} \]
\[\begin{gathered} {\text{Area of the Square}} = {\text{Area of }}\Delta ABC + {\text{Area of }}\Delta ACD \\ \Rightarrow {\text{Area of the Square = }}\frac{{\text{1}}}{{\text{2}}}{a^2} + \frac{1}{2}{a^2} = {a^2} \\ \therefore {\text{Area of the Square = (one side}}{{\text{)}}^{\text{2}}} \\ \end{gathered} \]
Example:
A chess board contains $$64$$ equal squares and the area of each square is $$6.25$$ square cm. A border around the board is $$2$$cm wide. Find the length of the side of the chess board.
Solution:
There are $$64$$ equal squares, each of area $$6.25$$ square cm.
The total area bounded by $$64$$ squares $$ = 64 \times 6.25 = 400$$ square cm.
One side of the square containing small squares $$ = \sqrt {400} = 20$$ cm.
The width of the border $$ = 2$$ cm.
The length of the side of the chess board $$ = 20 + 2(2) = 24$$ cm.
