Area of a Regular Polygon 2
Area of a regular polygon of n sides when the radius r of the inscribed circle is given
Since $$\angle AOB = \frac{{{{360}^ \circ }}}{n}$$
$$\therefore $$ the area of the polygon $$ = n \times $$area of the $$\Delta AOB = n \times \frac{{AB \times OD}}{2}$$
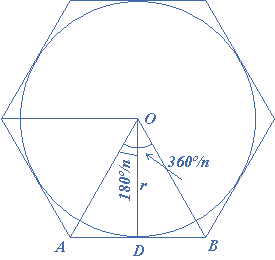
But $$OD = r$$, $$\frac{{AD}}{{OD}} = \tan \frac{{{{180}^ \circ }}}{n}$$
$$\therefore $$ $$AD = OD\tan \frac{{{{180}^ \circ }}}{n}$$ and $$AD = 2r\tan \frac{{{{180}^ \circ }}}{n}$$
Hence, the area of the regular polygon $$ = n \times \frac{{2r\tan \frac{{{{180}^ \circ }}}{n} \times r}}{2} = n{r^2}\tan \frac{{{{180}^ \circ }}}{n}$$
Also, the perimeter of the polygon $$ = nAB = n{\text{ }}2r\tan \frac{{{{180}^ \circ }}}{n} = 2nr\tan \frac{{{{180}^ \circ }}}{n}$$
(Using $$AB$$ from above)
\[ \begin{gathered} A = n{r^2}\tan \frac{{{{180}^ \circ }}}{n} \\ P = 2{\text{ }}nr\tan \frac{{{{180}^ \circ }}}{n} \\ \end{gathered} \]
Example:
A regular octagon circumscribed a circle of $$2m$$ radius. Find the area of the octagon.
Solution:
Here $$n = 8$$, $$r = 2m$$
$$\therefore $$ the area of the polygon $$ = n{r^2}\tan \frac{{{{180}^ \circ }}}{n} = 8 \times {(2)^2}\tan \frac{{{{180}^ \circ }}}{8} = 8 \times 4 \times \tan {22.5^ \circ }$$
$$\therefore $$ the area of the polygon$$ = 32 \times 0.4142 = 13.3 = 13.2544 = $$ square meters, approximately.
